Ludion
De Wikidebrouillard.
(→'''Matériel''') |
|||
| (9 versions intermédiaires masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{avertissement}} | {{avertissement}} | ||
| + | |||
| + | {{UPGRADE}} | ||
== '''Matériel''' == | == '''Matériel''' == | ||
| - | * [[Image:Bouteille.jpg|50px]] Une [[bouteille]] en plastique (soda, 1,5 | + | * [[Image:Bouteille.jpg|50px]] Une [[bouteille]] en plastique (soda, 1,5 L) |
* [[Image:Eau.jpg|50px]] De l'[[eau]] | * [[Image:Eau.jpg|50px]] De l'[[eau]] | ||
| - | * | + | * [[Image:Paille.jpg|50px]]) Une paille (ou un [[tube]] de [[stylo]] à [[bille]]) |
| - | * [[Image:Trombone.jpg|50px]] Un ou plusieurs [[trombones]] | + | * [[Image:Trombone.jpg|50px]] Un ou plusieurs [[trombones|trombone(s)]] |
* [[Image:Scotch.jpg|50px]] Du [[scotch]] transparent | * [[Image:Scotch.jpg|50px]] Du [[scotch]] transparent | ||
* [[Image:Paire de ciseaux.jpg|50px]] Des [[ciseau]]x | * [[Image:Paire de ciseaux.jpg|50px]] Des [[ciseau]]x | ||
== '''L'expérience''' == | == '''L'expérience''' == | ||
| + | |||
| + | Un sous-marin en bouteille ! | ||
| + | |||
| + | ==='''En vidéo'''=== | ||
| + | |||
<videoflash type="dailymotion">6NHjuEYg8CyCalSoZ</videoflash> | <videoflash type="dailymotion">6NHjuEYg8CyCalSoZ</videoflash> | ||
<videoflash type="dailymotion">1KMFd01DydQJ6gU5H</videoflash> | <videoflash type="dailymotion">1KMFd01DydQJ6gU5H</videoflash> | ||
<videoflash type="dailymotion">x4tvzy&v3=1&related=1</videoflash> | <videoflash type="dailymotion">x4tvzy&v3=1&related=1</videoflash> | ||
| + | <videoflash type="dailymotion">xde2ao</videoflash> | ||
| + | |||
| + | ==='''La manipulation'''=== | ||
| + | |||
| + | <i>Construction du ludion avec un assemblage de trombone et de morceau de paille/corps de stylo.</i> | ||
| + | |||
| + | ==='''Que voit-on ?'''=== | ||
| + | |||
| + | Lorsque l'on presse la bouteille, le ludion descend. Plus la pression des mains est forte, plus le ludion descend. Il est possible de le stabiliser au milieu de la colonne d'eau en ajustant la force exercée. | ||
| + | |||
| + | == '''Explications''' == | ||
| + | |||
| + | ==='''De manière simple'''=== | ||
| + | |||
| + | Lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du ludion et le fait descendre. | ||
| + | |||
| + | ==='''Allons plus loin dans l'explication'''=== | ||
| + | |||
| + | Nous cherchons à déterminer les conditions dans lesquelles le ludion coule ou flotte. Pour cela, la démonstration se décompose en deux étapes. | ||
| - | + | Dans un premier, temps nous allons déterminer les conditions de flottabilité du ludion. | |
| - | + | Puis nous nous intéresserons au déséquilibre provoqué par le manipulateur lorsqu'il presse la bouteille. | |
[[Image:Expludion1.jpg|thumb|Bilan des forces]] [[Image:Expludion3.jpg|thumb|Le système crayon-trombone-air]] | [[Image:Expludion1.jpg|thumb|Bilan des forces]] [[Image:Expludion3.jpg|thumb|Le système crayon-trombone-air]] | ||
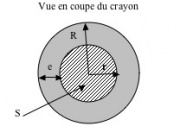
| - | [[Image:Expludion2.jpg|thumb|Vue en coupe du | + | [[Image:Expludion2.jpg|thumb|Vue en coupe du ludion]] |
| - | + | <i>Un souci d'activation de la fonction d'écriture mathématique rend la lecture des équations suivantes un peu difficile !</i> | |
| + | === '''À l'extérieur du ludion''' === | ||
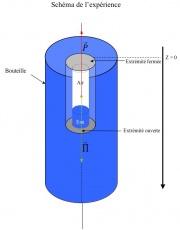
'''Bilan des forces qui s’appliquent sur le système crayon-trombone-air :''' | '''Bilan des forces qui s’appliquent sur le système crayon-trombone-air :''' | ||
| Ligne 30 : | Ligne 57 : | ||
Il est soumis à deux forces : | Il est soumis à deux forces : | ||
| - | + | * Son '''poids noté''' (dirigé vers le bas) : il a tendance à faire couler le système. | |
<math>\textstyle P=(m_{air}+m_{crayon}+m_{leste})g</math> | <math>\textstyle P=(m_{air}+m_{crayon}+m_{leste})g</math> | ||
| Ligne 48 : | Ligne 75 : | ||
| - | + | * La '''poussée d’Archimède notée''' (dirigée vers le haut) : elle a tendance à faire flotter le système. | |
| - | + | ||
| - | + | ||
<math>\textstyle \Pi=-(V_{air}+V_{crayon})\rho_{eau}g</math> | <math>\textstyle \Pi=-(V_{air}+V_{crayon})\rho_{eau}g</math> | ||
| Ligne 58 : | Ligne 83 : | ||
<math>\textstyle \Pi=-(2\pi eRl+\pi r^{2}x)\rho_{eau}g</math> | <math>\textstyle \Pi=-(2\pi eRl+\pi r^{2}x)\rho_{eau}g</math> | ||
| - | Remarque : on néglige la poussée d’Archimède sur le | + | Remarque : on néglige la poussée d’Archimède sur le lest, étant donné le faible volume occupé par celui-ci. |
| Ligne 69 : | Ligne 94 : | ||
On pose : <math>x_{0}=\frac{2eRl}{r^{2}}\left(\frac{\rho_{eau}-\rho_{crayon}}{\rho_{air}-\rho_{eau}}\right)-\frac{m_{leste}}{\pi r^{2}(\rho_{air}-\rho_{eau})}</math> | On pose : <math>x_{0}=\frac{2eRl}{r^{2}}\left(\frac{\rho_{eau}-\rho_{crayon}}{\rho_{air}-\rho_{eau}}\right)-\frac{m_{leste}}{\pi r^{2}(\rho_{air}-\rho_{eau})}</math> | ||
| - | + | À présent, on se place dans le cas réel où le système ne se trouve pas forcément à l’équilibre. | |
| - | + | Les forces se compensent alors plus ou moins. C’est ce qui provoque les mouvements du système dans la bouteille : | |
Le système monte lorsque : <math>\textstyle \Pi>P\Rightarrow x>x_{0}</math> | Le système monte lorsque : <math>\textstyle \Pi>P\Rightarrow x>x_{0}</math> | ||
| Ligne 78 : | Ligne 103 : | ||
Le système est immobile lorsque : <math>\textstyle \Pi=P\Rightarrow x=x_{0}</math> | Le système est immobile lorsque : <math>\textstyle \Pi=P\Rightarrow x=x_{0}</math> | ||
| - | La constante <math>\textstyle x_{0}</math> représente donc la hauteur limite de la colonne d’air à l’intérieur du | + | La constante <math>\textstyle x_{0}</math> représente donc la hauteur limite de la colonne d’air à l’intérieur du ludion, en deçà de laquelle le système descend au fond de la bouteille. On peut donc prévoir, en observant le niveau d'eau dans le crayon et en augmentant progressivement la pression de la main sur la bouteille, le moment où "le sous-marin va plonger". |
| - | On sait donc maintenant que c’est le volume d’air à l’intérieur du | + | On sait donc maintenant que c’est le volume d’air à l’intérieur du ludion qui conditionne son déplacement. Car seule la poussée d’Archimède, qui dépend de ce volume, peut contrer les effets de l’attraction gravitationnelle. |
| - | C’est bien le phénomène que l’on observe lors de l’expérience : lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du | + | C’est bien le phénomène que l’on observe lors de l’expérience : '''lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du ludion et le fait descendre.''' |
| - | Il se pose alors une nouvelle question : ''' | + | Il se pose alors une nouvelle question : '''Pourquoi le fait d’appuyer fait-il varier le niveau d’eau dans le crayon ?''' |
| - | === | + | === '''À l'intérieur du ludion''' === |
| - | [[Image:Expludion4.jpg|thumb|Forces de pression à l'intérieur du | + | [[Image:Expludion4.jpg|thumb|Forces de pression à l'intérieur du ludion]] |
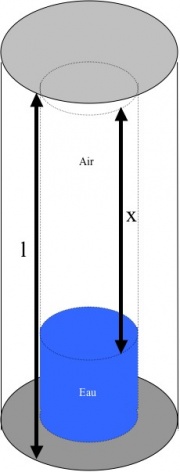
| - | Pour répondre à la question précédente, nous allons maintenant nous intéresser aux forces qui s’exercent sur la surface d’eau en contact avec l’air à l’intérieur du | + | Pour répondre à la question précédente, nous allons maintenant nous intéresser aux forces qui s’exercent sur la surface d’eau en contact avec l’air à l’intérieur du ludion. Ces forces résultent de la pression de l’air et de l’eau à cet endroit. |
Pour simplifier le problème, nous considérons l’air comme un gaz parfait. Nous pouvons donc déterminer la pression <math>\textstyle P_{air}</math> à partir de la relation des gaz parfaits : | Pour simplifier le problème, nous considérons l’air comme un gaz parfait. Nous pouvons donc déterminer la pression <math>\textstyle P_{air}</math> à partir de la relation des gaz parfaits : | ||
| Ligne 108 : | Ligne 133 : | ||
T est la température du gaz (K) | T est la température du gaz (K) | ||
| - | + | Au départ, avant de plonger le ludion dans l’eau, il contient n moles de gaz à la pression atmosphérique <math>P_{atm}</math>, d’où : | |
<math>n_{air}=\frac{P_{atm}V}{RT}</math> | <math>n_{air}=\frac{P_{atm}V}{RT}</math> | ||
| Ligne 117 : | Ligne 142 : | ||
| - | + | Et lorsque l’on plonge le ludion dans l’eau, la même quantité d’air est contenue à l’intérieur de celui-ci. En revanche, on remarque qu’à présent il y a un peu d’eau dans le ludion. Toujours d’après la loi des gaz parfaits, étant donné que seul le volume occupé par l’air a diminué, c’est la pression qui a augmenté : | |
<math>P_{air}=\frac{n_{air}RT}{V_{air}}</math> | <math>P_{air}=\frac{n_{air}RT}{V_{air}}</math> | ||
| Ligne 125 : | Ligne 150 : | ||
| - | + | Intéressons-nous maintenant à la pression exercée par la surface d’eau sur la surface d’air. Celle-ci se décompose en deux parties : la pression hydrostatique (celle subit par les plongeurs), et la pression exercée par le manipulateur. | |
| - | Si on considère l’eau comme un fluide incompressible alors la totalité de la force exercée sur les parois de la bouteille est transmise sur la surface air-eau. | + | Si on considère l’eau comme un fluide incompressible, alors la totalité de la force exercée sur les parois de la bouteille est transmise sur la surface air-eau. |
La pression hydrostatique est donnée par : <math>\textstyle P_{hydrostatique}=\rho_{eau}gz+P_{atm}</math> | La pression hydrostatique est donnée par : <math>\textstyle P_{hydrostatique}=\rho_{eau}gz+P_{atm}</math> | ||
| Ligne 136 : | Ligne 161 : | ||
Prenons le système à l’équilibre : <math>\textstyle F_{air}=F_{eau}</math> | Prenons le système à l’équilibre : <math>\textstyle F_{air}=F_{eau}</math> | ||
| - | + | Ces deux forces s’exercent sur une même surface. On en déduit que : <math>\textstyle P_{air}=P_{eau}</math> | |
| - | |||
D’où : <math>x=\frac{P_{atm}l}{\rho_{eau}gz+P_{atm}+P_{ext}}</math> (2) | D’où : <math>x=\frac{P_{atm}l}{\rho_{eau}gz+P_{atm}+P_{ext}}</math> (2) | ||
| Ligne 145 : | Ligne 169 : | ||
| - | + | ===''' Conclusion''' === | |
| - | === Conclusion === | + | |
| - | + | ||
| Ligne 157 : | Ligne 179 : | ||
Pour résumer : | Pour résumer : | ||
| - | |||
<center>'''Le système monte lorsque : <math>\textstyle F_{0}<F_{ext}</math>'''</center> | <center>'''Le système monte lorsque : <math>\textstyle F_{0}<F_{ext}</math>'''</center> | ||
| Ligne 164 : | Ligne 185 : | ||
<center>'''Le système est immobile lorsque : <math>\textstyle F_{0}=F_{ext}</math>'''</center> | <center>'''Le système est immobile lorsque : <math>\textstyle F_{0}=F_{ext}</math>'''</center> | ||
| - | |||
| - | |||
== '''Concepts scientifiques associés''' == | == '''Concepts scientifiques associés''' == | ||
| - | + | Ne pas hésiter à faire des liens avec l'encyclopédie : [http://fr.wikipedia.org/wiki/Accueil Wikipédia ] | |
| - | + | ||
| - | + | ||
== '''Liens avec d'autres expériences''' == | == '''Liens avec d'autres expériences''' == | ||
| - | ==='''Expériences sur | + | ==='''Expériences sur Wikidébrouillard'''=== |
* [[Ludion à distance]] | * [[Ludion à distance]] | ||
| Ligne 182 : | Ligne 199 : | ||
* [[Les Ballasts d'un sous-marin]] | * [[Les Ballasts d'un sous-marin]] | ||
| + | ==='''Autres expériences'''=== | ||
| - | + | Liens internet. Pourquoi ne pas [[Aide:Aide#Comment_cr.C3.A9er_une_nouvelle_page_.3F|créer la fiche expérience]] ! | |
| - | Liens internet. | + | |
| - | Pourquoi ne pas [[Aide:Aide#Comment_cr.C3.A9er_une_nouvelle_page_.3F|créer la fiche expérience]] ! | + | == '''Applications : liens avec le quotidien''' == |
| + | |||
| + | C'est un phénomène bien connu des plongeurs. En effet, plus le plongeur descend (donc plus la pression qui s'exerce sur lui augmente), plus il doit insuffler une quantité d'air importante dans sa bouée pour se stabiliser. | ||
| - | + | Par exemple, à 30m de profondeur la pression est de 4 bars (contre 1 bar à la surface). Le plongeur doit alors mettre 4 fois plus d'air dans sa bouée et ce pour un volume constant : à la surface comme au fond, la bouée du plongeur ne peut pas contenir plus de 40L d'air en moyenne. À 30 mètres de profondeur, on met l'équivalent de 40x4 litres d'air soit 160 litres d'air. | |
| - | == ''' | + | == '''Catégories''' == |
| - | |||
[[Catégorie:Physique]] | [[Catégorie:Physique]] | ||
| - | [[Catégorie: | + | [[Catégorie:mécanique]] |
| + | [[Catégorie:dynamique des fluides]] | ||
| + | [[Catégorie:poussée d'Archimède]] | ||
[[Catégorie:Contenus à développer]] | [[Catégorie:Contenus à développer]] | ||
[[Catégorie:Fiche à Valider]] | [[Catégorie:Fiche à Valider]] | ||
[[Catégorie:expérience]] | [[Catégorie:expérience]] | ||
Version actuelle en date du 18 décembre 2018 à 16:29
Sommaire |
Matériel
-
 Une bouteille en plastique (soda, 1,5 L)
Une bouteille en plastique (soda, 1,5 L)
-
 De l'eau
De l'eau
-
 ) Une paille (ou un tube de stylo à bille)
) Une paille (ou un tube de stylo à bille)
-
 Un ou plusieurs trombone(s)
Un ou plusieurs trombone(s)
-
 Du scotch transparent
Du scotch transparent
-
 Des ciseaux
Des ciseaux
L'expérience
Un sous-marin en bouteille !
En vidéo
La manipulation
Construction du ludion avec un assemblage de trombone et de morceau de paille/corps de stylo.
Que voit-on ?
Lorsque l'on presse la bouteille, le ludion descend. Plus la pression des mains est forte, plus le ludion descend. Il est possible de le stabiliser au milieu de la colonne d'eau en ajustant la force exercée.
Explications
De manière simple
Lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du ludion et le fait descendre.
Allons plus loin dans l'explication
Nous cherchons à déterminer les conditions dans lesquelles le ludion coule ou flotte. Pour cela, la démonstration se décompose en deux étapes.
Dans un premier, temps nous allons déterminer les conditions de flottabilité du ludion.
Puis nous nous intéresserons au déséquilibre provoqué par le manipulateur lorsqu'il presse la bouteille.
Un souci d'activation de la fonction d'écriture mathématique rend la lecture des équations suivantes un peu difficile !
À l'extérieur du ludion
Bilan des forces qui s’appliquent sur le système crayon-trombone-air :
Il est soumis à deux forces :
- Son poids noté (dirigé vers le bas) : il a tendance à faire couler le système.
<math>\textstyle P=(m_{air}+m_{crayon}+m_{leste})g</math>
Avec : <math>\textstyle m_{air}=\rho_{air}.V_{air}=\rho_{air}.\pi r^{2}x</math>
<math>\textstyle m_{crayon}=\rho_{crayon}.V_{crayon}=\rho_{crayon}.2\pi eRl</math>
Notations :
g = Accélération de la pesanteur <math>\rho</math> = Masse volumique V = Volume m = Masse
On obtient : <math>\textstyle P=(\rho_{air}.\pi r^{2}x+\rho_{crayon}.2\pi eRl+m_{leste})g</math>
- La poussée d’Archimède notée (dirigée vers le haut) : elle a tendance à faire flotter le système.
<math>\textstyle \Pi=-(V_{air}+V_{crayon})\rho_{eau}g</math>
On obtient :
<math>\textstyle \Pi=-(2\pi eRl+\pi r^{2}x)\rho_{eau}g</math>
Remarque : on néglige la poussée d’Archimède sur le lest, étant donné le faible volume occupé par celui-ci.
Pour commencer, on considère le système à l’équilibre et on applique la première loi de Newton. Les forces sont toutes parallèles à l'axe z donc : <math>P-\Pi =0</math>
On obtient : <math>\textstyle P=(\rho_{air}.\pi r^{2}x+\rho_{crayon}.2\pi eRl+m_{leste})g-(2\pi eRl+\pi r^{2}x)\rho_{eau}g=0</math>
Soit : <math>x=\frac{2eRl}{r^{2}}\left(\frac{\rho_{eau}-\rho_{crayon}}{\rho_{air}-\rho_{eau}}\right)-\frac{m_{leste}}{\pi r^{2}(\rho_{air}-\rho_{eau})}</math> (1)
On pose : <math>x_{0}=\frac{2eRl}{r^{2}}\left(\frac{\rho_{eau}-\rho_{crayon}}{\rho_{air}-\rho_{eau}}\right)-\frac{m_{leste}}{\pi r^{2}(\rho_{air}-\rho_{eau})}</math>
À présent, on se place dans le cas réel où le système ne se trouve pas forcément à l’équilibre. Les forces se compensent alors plus ou moins. C’est ce qui provoque les mouvements du système dans la bouteille :
Le système monte lorsque : <math>\textstyle \Pi>P\Rightarrow x>x_{0}</math>
Le système descend lorsque : <math>\textstyle \Pi<P\Rightarrow x<x_{0}</math>
Le système est immobile lorsque : <math>\textstyle \Pi=P\Rightarrow x=x_{0}</math>
La constante <math>\textstyle x_{0}</math> représente donc la hauteur limite de la colonne d’air à l’intérieur du ludion, en deçà de laquelle le système descend au fond de la bouteille. On peut donc prévoir, en observant le niveau d'eau dans le crayon et en augmentant progressivement la pression de la main sur la bouteille, le moment où "le sous-marin va plonger".
On sait donc maintenant que c’est le volume d’air à l’intérieur du ludion qui conditionne son déplacement. Car seule la poussée d’Archimède, qui dépend de ce volume, peut contrer les effets de l’attraction gravitationnelle.
C’est bien le phénomène que l’on observe lors de l’expérience : lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du ludion et le fait descendre.
Il se pose alors une nouvelle question : Pourquoi le fait d’appuyer fait-il varier le niveau d’eau dans le crayon ?
À l'intérieur du ludion
Pour répondre à la question précédente, nous allons maintenant nous intéresser aux forces qui s’exercent sur la surface d’eau en contact avec l’air à l’intérieur du ludion. Ces forces résultent de la pression de l’air et de l’eau à cet endroit.
Pour simplifier le problème, nous considérons l’air comme un gaz parfait. Nous pouvons donc déterminer la pression <math>\textstyle P_{air}</math> à partir de la relation des gaz parfaits :
<math>\textstyle PV=nRT</math>
Où : P est la pression du gaz (Pa)
V est le volume occupé par le gaz (m3)
n est la quantité de gaz contenu dans ce volume (mole)
R est la constante des gaz parfaits : R = 8,314 Pa.m3.mole-1.K-1
T est la température du gaz (K)
Au départ, avant de plonger le ludion dans l’eau, il contient n moles de gaz à la pression atmosphérique <math>P_{atm}</math>, d’où :
<math>n_{air}=\frac{P_{atm}V}{RT}</math>
avec V : le volume intérieur (« vide ») du crayon
<math>n_{air}=\frac{P_{atm}.\pi r^{2}l}{RT}</math>
Et lorsque l’on plonge le ludion dans l’eau, la même quantité d’air est contenue à l’intérieur de celui-ci. En revanche, on remarque qu’à présent il y a un peu d’eau dans le ludion. Toujours d’après la loi des gaz parfaits, étant donné que seul le volume occupé par l’air a diminué, c’est la pression qui a augmenté :
<math>P_{air}=\frac{n_{air}RT}{V_{air}}</math>
D’où : <math>P_{air}=P_{atm}\left(\frac{l}{x}\right)</math>
Intéressons-nous maintenant à la pression exercée par la surface d’eau sur la surface d’air. Celle-ci se décompose en deux parties : la pression hydrostatique (celle subit par les plongeurs), et la pression exercée par le manipulateur.
Si on considère l’eau comme un fluide incompressible, alors la totalité de la force exercée sur les parois de la bouteille est transmise sur la surface air-eau.
La pression hydrostatique est donnée par : <math>\textstyle P_{hydrostatique}=\rho_{eau}gz+P_{atm}</math>
La pression exercée par le manipulateur sur le fluide est donnée par : <math>P_{ext}=\frac{F_{ext}}{\pi r^{2}}</math>
D’où : <math>P_{eau}=\rho_{eau}gz+P_{atm}+\frac{F_{ext}}{\pi r^{2}}</math>
Prenons le système à l’équilibre : <math>\textstyle F_{air}=F_{eau}</math> Ces deux forces s’exercent sur une même surface. On en déduit que : <math>\textstyle P_{air}=P_{eau}</math>
D’où : <math>x=\frac{P_{atm}l}{\rho_{eau}gz+P_{atm}+P_{ext}}</math> (2)
On vient donc de relier la hauteur de la colonne d’air dans le stylo avec la pression exercée par le manipulateur sur la bouteille.
Conclusion
En combinant les équations (1) et (2), on peut alors définir la valeur minimum <math>\textstyle F_{0}</math> de <math>\textstyle F_{ext}</math> nécessaire pour faire couler le stylo :
Pour résumer :
Concepts scientifiques associés
Ne pas hésiter à faire des liens avec l'encyclopédie : Wikipédia
Liens avec d'autres expériences
Expériences sur Wikidébrouillard
Autres expériences
Liens internet. Pourquoi ne pas créer la fiche expérience !
Applications : liens avec le quotidien
C'est un phénomène bien connu des plongeurs. En effet, plus le plongeur descend (donc plus la pression qui s'exerce sur lui augmente), plus il doit insuffler une quantité d'air importante dans sa bouée pour se stabiliser.
Par exemple, à 30m de profondeur la pression est de 4 bars (contre 1 bar à la surface). Le plongeur doit alors mettre 4 fois plus d'air dans sa bouée et ce pour un volume constant : à la surface comme au fond, la bouée du plongeur ne peut pas contenir plus de 40L d'air en moyenne. À 30 mètres de profondeur, on met l'équivalent de 40x4 litres d'air soit 160 litres d'air.
Catégories
- Dernière modification de cette page le 18 décembre 2018 à 16:29.
- Cette page a été consultée 67 550 fois.
- Contenu disponible sous Creative Commons - Paternite Partage a l'identique (CC-BY-SA).
- Politique de confidentialité
- À propos de Wikidebrouillard
- Avertissements