Gamme infinie
De Wikidebrouillard.
m (a renommé Une gamme infinie en Gamme infinie: article devant le nom) |
(→Application : Lien avec le quotidien) |
||
| (10 versions intermédiaires masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{avertissement}} | {{avertissement}} | ||
| + | |||
| + | == '''Présentation de l'expérience''' == | ||
| + | |||
| + | Quelques notes jouées en boucle donnent l'impression d'une gamme infinie. Hein ? C'est possible ça ? | ||
== '''Matériel''' == | == '''Matériel''' == | ||
| + | |||
* De quoi écouter en stéréo un son. | * De quoi écouter en stéréo un son. | ||
| - | * Cette fiche | + | * Cette fiche. |
== '''L'expérience''' == | == '''L'expérience''' == | ||
| + | |||
==='''En vidéo'''=== | ==='''En vidéo'''=== | ||
| + | |||
==='''Pas de vidéo, l'expérience est à faire en direct'''=== | ==='''Pas de vidéo, l'expérience est à faire en direct'''=== | ||
==='''La manipulation'''=== | ==='''La manipulation'''=== | ||
| - | + | ||
| + | Écouter ceci en boucle : | ||
<mp3>Gamme_infinie.mp3</mp3> | <mp3>Gamme_infinie.mp3</mp3> | ||
| - | ==='''Que voit-on ?=== | + | ==='''Que voit-on ?'''=== |
| + | |||
On ne voit rien !! C'est sonore ! | On ne voit rien !! C'est sonore ! | ||
[[Image:Sonagramme.jpg]] | [[Image:Sonagramme.jpg]] | ||
| - | On a l'impression que la gamme monte (do, ré, mi, fa, sol, la,....) à l' | + | On a l'impression que la gamme monte (do, ré, mi, fa, sol, la,....) à l'infini !! |
== '''Explication''' == | == '''Explication''' == | ||
| - | + | ||
| + | Cette gamme infinie est aussi appelée gamme de Shepard. | ||
| + | |||
| + | Le texte suivant est issue de [http://fr.wikipedia.org/wiki/Gamme_de_Shepard Wikipédia] : | ||
| + | |||
| + | En dehors de leur aspect curieux ou ludique, les sons de Shepard servent pour les expériences sur la perception de la hauteur musicale des sons. | ||
| + | |||
| + | La gamme de Shepard, en tant que perception paradoxale, peut se comparer à l'objet impossible appelé escalier de Penrose, pour la perspective. | ||
| + | |||
| + | [[Fichier:Escalierpenrose.svg]] | ||
| + | |||
| + | Comme nous ne pouvons pas admettre qu'un son monte sans fin tout en se reproduisant périodiquement égal à lui-même, nous sommes amenés à remettre en cause soit notre perception, comme lorsqu'un ventriloque donne l'illusion que la voix sort de la bouche de bois de sa marionette, soit les règles dont nous croyions qu'elles les dirigent, comme quand, confrontés au paradoxe du barbier, nous concluons qu'un tel règlement ne peut s'appliquer3. « Ce qui est une illusion, c’est d’assimiler la hauteur, une expérience subjective, l’écoute, à la fréquence, paramètre objectif et mesurable », conclut Jean-Claude Risset4. | ||
| + | |||
| + | Les études psychoacoustiques ont abouti à la conclusion que la perception de la hauteur peut se décomposer en hauteur spectrale, une sensation approximative du caractère grave ou aigu d'un son, indépendant de l'existence ou non d'une fréquence fondamentale, et hauteur fondamentale ou chroma, beaucoup plus précise, mais sujette à des erreurs d'octave. En demandant à des personnes d'évaluer les relations d'intervalle entre des sons de Shepard, les expérimentateurs s'adressent exclusivement à la perception de la hauteur fondamentale, puisque tous les sons de Shepard ont leur énergie répartie dans l'ensemble du spectre audible5. | ||
| + | |||
| + | Diana Deutsch a ainsi présenté successivement à des sujets des sons de Shepard éloignés d'un intervalle de trois tons, soit une demi-octave. Les sujets ont nettement désigné certaines notes comme plus aigües. Si les sensations de hauteur spectrale et de hauteur fondamentale étaient indépendantes, les auditeurs n'auraient pu choisir entre trois tons montants et trois tons descendants. Il s'est avéré, de plus, que le son de Shepard désigné comme le plus aigu varie d'une personne à l'autre, et se trouve corrélé avec le dialecte parlé par les sujets participants. L'expérience montre que le principe de l'équivalence perceptive d'une transposition n'est pas universel, et que les sujets ont en général une certaine forme d'oreille absolue6. | ||
== '''Questions sans réponses''' == | == '''Questions sans réponses''' == | ||
| Ligne 31 : | Ligne 55 : | ||
== '''Application : Lien avec le quotidien''' == | == '''Application : Lien avec le quotidien''' == | ||
| - | + | IL semble que la musique de Super Mario 64, dans l'escalier "infini" soit une gamme Shepard. A votre avis ? est-ce le cas ? | |
| + | |||
| + | <videoflash type="youtube" num="12">KwDA5eJJz0U|400|300</videoflash> | ||
== '''Liens avec d'autres expériences''' == | == '''Liens avec d'autres expériences''' == | ||
| - | [[Deux sons continus donnent une modulation]] | + | * [[Deux sons continus donnent une modulation]] |
| - | [[Sonnerie anti-jeunes]] | + | * [[Sonnerie anti-jeunes]] |
| + | |||
| + | Sur un autre site : [http://www.cochlea.org/entendre/la-gamme-infinie-illusion-auditive Cochlea.org] | ||
| + | |||
| + | == '''Catégories''' == | ||
| - | |||
[[Catégorie:Physique]] | [[Catégorie:Physique]] | ||
| - | |||
[[Catégorie:Contenus à développer]] | [[Catégorie:Contenus à développer]] | ||
[[Catégorie:Fiche à Valider]] | [[Catégorie:Fiche à Valider]] | ||
[[Catégorie:expérience]] | [[Catégorie:expérience]] | ||
[[Catégorie:Acoustique]] | [[Catégorie:Acoustique]] | ||
Version actuelle en date du 5 décembre 2014 à 16:38
Sommaire[masquer] |
Présentation de l'expérience
Quelques notes jouées en boucle donnent l'impression d'une gamme infinie. Hein ? C'est possible ça ?
Matériel
- De quoi écouter en stéréo un son.
- Cette fiche.
L'expérience
En vidéo
Pas de vidéo, l'expérience est à faire en direct
La manipulation
Écouter ceci en boucle :
Que voit-on ?
On ne voit rien !! C'est sonore !
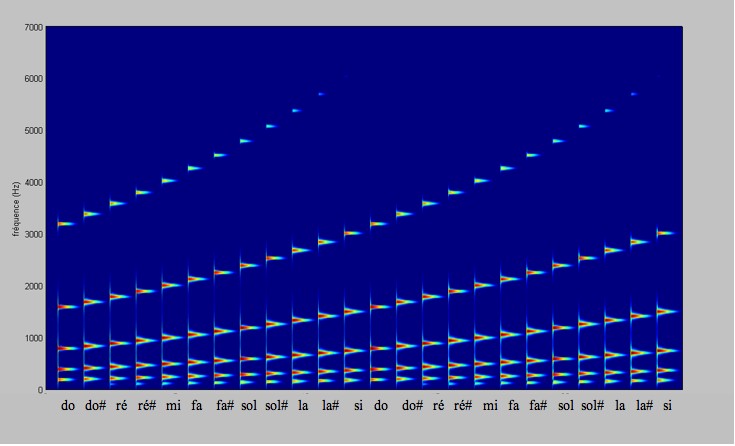
On a l'impression que la gamme monte (do, ré, mi, fa, sol, la,....) à l'infini !!
Explication
Cette gamme infinie est aussi appelée gamme de Shepard.
Le texte suivant est issue de Wikipédia :
En dehors de leur aspect curieux ou ludique, les sons de Shepard servent pour les expériences sur la perception de la hauteur musicale des sons.
La gamme de Shepard, en tant que perception paradoxale, peut se comparer à l'objet impossible appelé escalier de Penrose, pour la perspective.
| Erreur lors de la création de la miniature : Unable to run external programs in safe mode. |
Comme nous ne pouvons pas admettre qu'un son monte sans fin tout en se reproduisant périodiquement égal à lui-même, nous sommes amenés à remettre en cause soit notre perception, comme lorsqu'un ventriloque donne l'illusion que la voix sort de la bouche de bois de sa marionette, soit les règles dont nous croyions qu'elles les dirigent, comme quand, confrontés au paradoxe du barbier, nous concluons qu'un tel règlement ne peut s'appliquer3. « Ce qui est une illusion, c’est d’assimiler la hauteur, une expérience subjective, l’écoute, à la fréquence, paramètre objectif et mesurable », conclut Jean-Claude Risset4.
Les études psychoacoustiques ont abouti à la conclusion que la perception de la hauteur peut se décomposer en hauteur spectrale, une sensation approximative du caractère grave ou aigu d'un son, indépendant de l'existence ou non d'une fréquence fondamentale, et hauteur fondamentale ou chroma, beaucoup plus précise, mais sujette à des erreurs d'octave. En demandant à des personnes d'évaluer les relations d'intervalle entre des sons de Shepard, les expérimentateurs s'adressent exclusivement à la perception de la hauteur fondamentale, puisque tous les sons de Shepard ont leur énergie répartie dans l'ensemble du spectre audible5.
Diana Deutsch a ainsi présenté successivement à des sujets des sons de Shepard éloignés d'un intervalle de trois tons, soit une demi-octave. Les sujets ont nettement désigné certaines notes comme plus aigües. Si les sensations de hauteur spectrale et de hauteur fondamentale étaient indépendantes, les auditeurs n'auraient pu choisir entre trois tons montants et trois tons descendants. Il s'est avéré, de plus, que le son de Shepard désigné comme le plus aigu varie d'une personne à l'autre, et se trouve corrélé avec le dialecte parlé par les sujets participants. L'expérience montre que le principe de l'équivalence perceptive d'une transposition n'est pas universel, et que les sujets ont en général une certaine forme d'oreille absolue6.
Questions sans réponses
Concepts scientifiques associés
Ici c'est pour aller plus loin.
ne pas hésiter à faire des liens avec l'encyclopédie :Wikipédia
Application : Lien avec le quotidien
IL semble que la musique de Super Mario 64, dans l'escalier "infini" soit une gamme Shepard. A votre avis ? est-ce le cas ?
Liens avec d'autres expériences
Sur un autre site : Cochlea.org
Catégories
CO
Gamme infinie
Quelques notes jouées en boucle donnent l'impression d'une gamme infinie. Hein ? C'est possible ça ?
- Dernière modification de cette page le 5 décembre 2014 à 16:38.
- Cette page a été consultée 33 243 fois.
- Contenu disponible sous Creative Commons - Paternite Partage a l'identique (CC-BY-SA).
- Politique de confidentialité
- À propos de Wikidebrouillard
- Avertissements

