Les 3 portes
De Wikidebrouillard.
(→Allons plus loin dans l'explication) |
(→Allons plus loin dans l'explication) |
||
| Ligne 47 : | Ligne 47 : | ||
[[Image:dessinsim1.jpg]] | [[Image:dessinsim1.jpg]] | ||
Avec la technique de l'expérience : | Avec la technique de l'expérience : | ||
| + | [[Image:dessinsim2.jpg]] | ||
== '''Liens avec d'autres expériences''' == | == '''Liens avec d'autres expériences''' == | ||
Version du 10 janvier 2011 à 18:31
Mettre à la place de "codedailymotion" le code qui se trouve dans le lien que donne Dailymotion.
==Présentation de l'expérience==Le joueur des trois portes confirmé sait qu'il a plus d'une chance sur deux de trouver le bon bol sous lequel est caché l'objet!
Sommaire |
Matériel
-
Un bol ou n'importe quoi sous lequel on peut cacher quelque chose.
-
Une balle ou un autre petit objet.
- ...
L'expérience
L'expérience du jeu des 3 portes illustre ce qu'est une probabilité. Attention, au début ça peut paraître bizarre, c'est pourquoi on peut analyser cette expérience pour comprendre.
La manipulation
1) Je place 3 bols (si vous êtes fâchés contre les bols, prenez des chapeaux par exemple) sur la table. Sous un des trois bols, il y a une balle de cachée. Mon cobaye ne sait bien sûr pas sous quel bol la balle est cachée.
2) Je demande à mon cobaye de choisir un bol en vue de deviner où est la balle.
3) J'enlève un des bols qui n'a PAS la balle. J'informe mon cobaye.
4) Le cobaye (qui est le joueur...) peut alors changer son choix ou garder le même bol. Je lui demande son choix.
5) Moment de vérité!
Que voit-on ?
Si votre cobaye est un joueur professionnel des trois portes, il vous dira qu'il a plus de chance de tomber sur la balle si il change son choix.
Le mauvais joueur vous dira que de toute façon, comme il n'y a plus que deux bols,c'est comme à pile ou face, à ce point il n'y a qu'une chance sur deux de gagner.
Explications
De manière simple
A la première étape, il y a un bol rempli et deux bol vides, donc on a plus de chances de se tromper. Du coup, à la deuxième étape, comme on est sûr qu'un des deux bols est rempli et comme le bol que l'on a choisi est sans doute vide, autant changer.
Questions sans réponses
Ici je mets les questions soulevées par l'expérience, qui n'ont pas trouvé de réponses !!
Allons plus loin dans l'explication
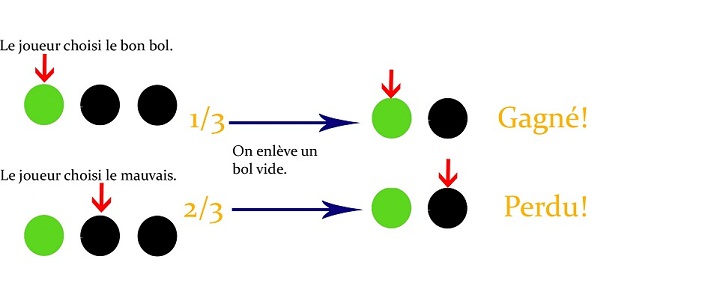
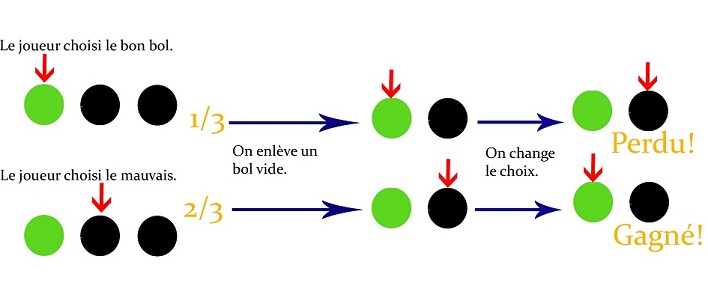
Regardons les probabilités : au départ, une chance sur 3 de choisir le bon bol. Sur le schéma, le bon bol est en vert et le bol choisi a une flèche pointée sur sa tête.
Ensuite, cela dépend de la technique utilisée.
Avec la technique normale :
Avec la technique de l'expérience :
Liens avec d'autres expériences
Expériences sur Wikidébrouillard
Indiquer ici les expériences de Wikidébrouillard.
Autres expériences
Autres expériences avec le même concept, recherche sur internet (indiquer les liens).
Applications : liens avec le quotidien
C'est de la culture, ça aide à comprendre le monde !! N'hésitez pas à lancer la discussion de votre fiche (après l'avoir sauvegarder !) afin de trouver de l'aide pour la compléter
Lieux propices à sa réalisation
Indiquer ici des lieux où tout le matériel nécessaire pour réaliser cette expérience est disponible.
Catégories
Penser à fixer les disciplines scientifiques qui correspondent à l'expérience. Remplacer "à classer" par la discipline correspondante.
S'inscrire
Login
Aide
