Tracé de parabole
De Wikidebrouillard.
Sommaire |
Présentation de l'expérience
Comment Harel de la Noé a-t-il tracé la parabole de la gare de St Brieuc ?
Matériel
- planche à dessin, calendrier, carton...
-
crayon
- punaises
- chaînette du rayon bricolage, laisse de chien ...
- la photo de la gare de St Brieuc ;)
L'expérience
En vidéo
La manipulation
- acrocher les deux extrémités de la chainette sur la planche à dessin avec les punaises
- mettre la planche verticale et laisser l'attraction terrestre faire son boulot
- prendre le crayon et tracer la parabole en suivant la chainette
- retourner le tracé
- comparez avec votre photo de la gare
- émotion...
Que voit-on ?
Comme la chaîne n'est pas tendue, elle semble tomber et a une forme géométrique symétrique. C'est la même figure que l'on retrouve en architecture pour les arcs, les voûtes, et beaucoup d'autres encore. Toutefois, avec des chaînes, les paraboles sont concaves (la chaîne tend vers le bas) tandis que dans la plupart des constructions, celles-ci sont convexes.
Explications
De manière simple
Le poids impose à la chaîne de tomber. Toutefois, celle ci est retenue verticalement à ses extrémités, on obtient donc une forme de parabole. La force exercée par la terre, c'est-à-dire le poids, la tension des maillons de la chaîne et la réaction du support, ici le mur, doivent se compenser pour respecter les loi de la mécanique. Au niveau du centre de gravité, c'est-à-dire au milieu de la chaîne, le poids est maximal. Seule la réaction du mur empêche la chaîne de tomber.
Le résultat serait similaire avec un quelconque fil subissant l'attraction terrestre. C'est comme les vieux ponts suspendus en corde (par exemple chez las anciennes civilisations incas ou aztèques) ou en bois qui se balancent au-dessus du vide, entre deux parois verticales : la forme reste parabolique.
On pourrait faire la même chose en utilisant une autre force que le poids. Par exemple, un ballon qui se gonfle prend également une telle forme, mais dans ce cas, c'est la pression de l'air qui provoque la déformation.
ATTENTION : LA FORME DE LA CHAINE N'EST PAS UNE PARABOLE A LA DIFFÉRENCE DES ARCHES DES PONTS OU DES FIGURES LUMINEUSES OBSERVABLES SUR LES MURS. MAIS NOUS VERRONS LA SUBTILE DIFFÉRENCE CI-DESSOUS.
Questions sans réponses
- Pourquoi certaines paraboles sont-elles plus accentuées que d'autres?
- D'où vient le terme "parabole"?
- Quelle est la fonction mathématique qui permet d'approximer les paraboles?
Allons plus loin dans l'explication
Définition de la parabole sur Wikipédia
La chaînette est la forme prise par un fil pesant flexible infiniment mince homogène inextensible suspendu entre deux points, placé dans un champ de pesanteur uniforme ; Galilée pensait que c'était un arc de parabole, mais Leibniz, Jean Bernoulli, et Huygens ont montré en 1691, indépendamment, qu'il n'en était rien. ` En réalité, il ne s'agit pas de paraboles mais de "chainettes".les équations de la parabole étant différentes des équations de la chaînette.Les tracés sont également différents. Apprenons à différencier les chaînettes des paraboles : pour une même longueur les paraboles sont plus pointues.
Intéressons nous à l'équation d'équilibre des forces de la chainette.En considérant le schéma suivant:
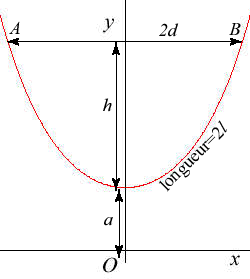
La relation entre la longueur 2l, la flèche h et la largeur 2d
est donnée par :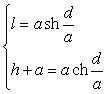 
, d'où en éliminant
, la relation :
, soit,
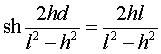
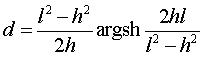
On obtient l'équation cartésienne suivante: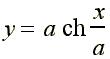
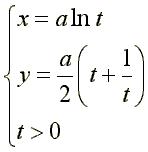
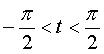
L'axe des x en est la base, celui des y, l’axe de symétrie, avec la paramétrisation cartésienne suivante:
avec
Puis, avec la représentation suivante nous mettons en scène les forces effectives: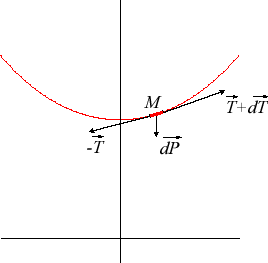
Avec les notations de la figure ci-dessus ( 
= tension du fil en M, m = masse linéique du fil) , écrivons que la somme des forces en M est nulle (principe fondamental de la dynamique):
On peut alors écrire que 
,et, en intégrant,
On déduit alors que 
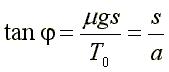
Nous pouvons affirmer qu'un pont suspendu par ses câbles suit un arc de parabole : si nous remplaçons la masse mds par la masse mdx (en supposant que la masse des câbles est négligeable devant celle du pont).On obtient alors l'équation différentielle suivante: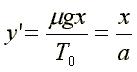
qui donne par intégration une parabole.
Liens avec d'autres expériences
Expériences sur Wikidébrouillard
Balade thématique sur le patrimoine scientifique et technique
Autres expériences
Liens internet.
Pourquoi ne pas créer la fiche expérience !
Applications : liens avec le quotidien
- Les fils électriques suspendus au dessus du vide
- Les ponts en corde dont le sol est en planches de bois
- Les équilibristes sur certains câbles.
- Un hamac.
S'inscrire
Login
Aide
