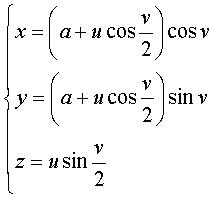Anneau de Moebius
De Wikidebrouillard.
(→Concepts scientifiques associés) |
m |
||
| Ligne 12 : | Ligne 12 : | ||
==='''La manipulation'''=== | ==='''La manipulation'''=== | ||
| - | + | * Découper une bande dans la feuille de papier. | |
| - | + | * Réunir les deux extrémités de la bande en faisant juste un demi-tour avant de les rassembler. | |
| - | + | * Fermer la boucle obtenue avec le ruban adhésif. | |
| - | + | ||
| - | + | ||
==='''Que voit-on ?=== | ==='''Que voit-on ?=== | ||
| - | + | * Avec le stylo, tracer une ligne sur une seule face. SURPRISE : il n'y a qu'une seule face ! | |
| - | + | * Suivre avec le doigt un côté du ruban. RE-SURPRISE : il n'y a qu'un seul côté ! | |
| - | Donc cet objet en | + | Donc cet objet en trois dimensions (il a une hauteur, une largeur et une profondeur), n'a qu''''un côté''' et qu''''une face''' !! |
| Ligne 39 : | Ligne 37 : | ||
* Sur la page [http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius Ruban de Moebius] de Wikipédia, vous trouverez plus d'explications et des animations de différentes torsions. | * Sur la page [http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius Ruban de Moebius] de Wikipédia, vous trouverez plus d'explications et des animations de différentes torsions. | ||
| - | * [http://www.mathcurve.com/surfaces/mobius/mobius.shtml L'anneau de | + | * [http://www.mathcurve.com/surfaces/mobius/mobius.shtml L'anneau de Moebius] sur le site de mathcurve. |
== '''Applications : Liens avec le quotidien''' == | == '''Applications : Liens avec le quotidien''' == | ||
| Ligne 63 : | Ligne 61 : | ||
[[Catégorie:art]] | [[Catégorie:art]] | ||
[[Catégorie:Architecture]] | [[Catégorie:Architecture]] | ||
| - | |||
[[Catégorie:Contenus à développer]] | [[Catégorie:Contenus à développer]] | ||
[[Catégorie:Fiche à Valider]] | [[Catégorie:Fiche à Valider]] | ||
[[Catégorie:expérience]] | [[Catégorie:expérience]] | ||
[[Catégorie:mediaspip]] | [[Catégorie:mediaspip]] | ||
Version du 4 octobre 2012 à 13:00
Sommaire |
Matériel
-
Une feuille de papier
-
Une paire de ciseaux
-
Du scotch
-
Un crayon
L'expérience
La manipulation
- Découper une bande dans la feuille de papier.
- Réunir les deux extrémités de la bande en faisant juste un demi-tour avant de les rassembler.
- Fermer la boucle obtenue avec le ruban adhésif.
Que voit-on ?
- Avec le stylo, tracer une ligne sur une seule face. SURPRISE : il n'y a qu'une seule face !
- Suivre avec le doigt un côté du ruban. RE-SURPRISE : il n'y a qu'un seul côté !
Donc cet objet en trois dimensions (il a une hauteur, une largeur et une profondeur), n'a qu'un côté et qu'une face !!
Explication
Cet anneau a la particularité de ne posséder qu'un seul bord et qu'une seule face. C'est une figure non-orientable. Cela signifie qu'on ne peut pas lui donner un sens de parcours comme on pourrait le faire avec un cylindre de révolution finie, par exemple, qui lui possède bien deux faces (l'intérieur et l'extérieur du cylindre) et deux bords (le haut et le bas du cylindre).
L'anneau de Moebius peut être défini comme étant une surface fermée dont le bord se réduit à un cercle.
Concepts scientifiques associés
En général, nous considérons comme Anneau de Moebius toute construction avec un nombre impair de demi-tours.
Paramétrisation cartésienne :
- Sur la page Ruban de Moebius de Wikipédia, vous trouverez plus d'explications et des animations de différentes torsions.
- L'anneau de Moebius sur le site de mathcurve.
Applications : Liens avec le quotidien
Applications en images !
 |
 |
 |
 |
 |
 |
S'inscrire
Login
Aide
