Planche de Galton
De Wikidebrouillard.
(→'''La manipulation''') |
(→'''La manipulation''') |
||
| Ligne 27 : | Ligne 27 : | ||
Précautions à prendre: | Précautions à prendre: | ||
| + | |||
- Les écarts entre les clous ne doivent pas être beaucoup plus grands que le diamètre des billes, pour ne pas fausser les probabilités. | - Les écarts entre les clous ne doivent pas être beaucoup plus grands que le diamètre des billes, pour ne pas fausser les probabilités. | ||
| + | |||
- Une mauvaise implantation des clous a une incidence importante sur l'allure du résultat finale. | - Une mauvaise implantation des clous a une incidence importante sur l'allure du résultat finale. | ||
Version du 21 octobre 2009 à 10:49
Sommaire[masquer] |
Présentation de l'expérience
Cette expérience a pour objectif de montrer et de comprendre une règle de probabilité.
Matériel
- -carton
L'expérience
La manipulation
Des clous sont plantés sur la partie supérieure de la planche, de telle sorte qu'une bille lâchée sur la planche passe soit à droite soit à gauche pour chaque rangée de clous. Dans la partie inferieure les billes sont rassemblées en fonction du nombre de passages à gauche et de passage à droite qu'elles ont fait.
Précautions à prendre:
- Les écarts entre les clous ne doivent pas être beaucoup plus grands que le diamètre des billes, pour ne pas fausser les probabilités.
- Une mauvaise implantation des clous a une incidence importante sur l'allure du résultat finale.
Que voit-on ?
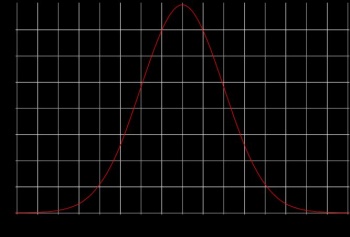
Apprêt plusieurs passage de billes on peut observer qu'elle s'accumules pour formé une courbe qui doit s'approcher d'une gaussienne.

Explications
De manière simple
Lorsque l'on fait tomber une bille, elle le choix de tomber à droit ou à gauche, il y a donc 0.5 de probabilité de chaque coté. La bille répète cette expérience plusieurs foi autant qu’il y a d’étage dans le pyramide. A la sortie de la bille elle a donc la possibilité de ce trouvé à plusieurs endroits, neuf dans le cas de l’expérience. A chaque cas est associée une probabilité propre. Ainsi en considérant qu’il y a un grand nombre de bille on peut déduire une courbe de probabilité qui s'approche de la forme d'une courbe de Gauss
Questions sans réponses
Allons plus loin dans l'explication
Chaque case correspond à un résultat possible d'une expérience binomiale (en tant qu'une expérience de Bernoulli répétée) et on peut remarquer que la répartition des billes dans les cases approche la forme d'une courbe de Gauss, autrement dit : la loi binomiale converge vers la loi normale. Il s'agit donc d'une illustration au théorème de Moivre-Laplace.
Liens avec d'autres expériences
Expériences sur Wikidébrouillard
Pas d'expériences de même nature sur wikidébrouillard.
Autres expériences
Petite animation de planche de galton sur ce lien http://maths.ac-orleans-tours.fr/tbi/planchegalton/galton.htm
Applications : liens avec le quotidien
C'est de la culture, ça aide à comprendre le monde !! N'hésitez pas à lancer la discussion de votre fiche (après l'avoir sauvegarder !) afin de trouver de l'aide pour la compléter
Lieux propices à sa réalisation
Dans petit atelier. Pas de précaution de sécurité particulière. Attention aux doigts.
Catégories
Penser à fixer les disciplines scientifiques qui correspondent à l'expérience. Remplacer "à classer" par la discipline correspondante.