Gaz parfaits
De Wikidebrouillard.
(→'''Concepts scientifiques associés''') |
(→'''Concepts scientifiques associés''') |
||
| Ligne 53 : | Ligne 53 : | ||
* N est le nombre de particules | * N est le nombre de particules | ||
* R est la constante des gaz parfaits | * R est la constante des gaz parfaits | ||
| - | R = 8,314 472 | + | R = 8,314 472 J/(K.mol) |
| - | on a en fait R = NA•kB où NA est le nombre d'[http://fr.wikipedia.org/wiki/Nombre_d'Avogadro Avogadro] (6,022×10 | + | on a en fait R = NA•kB où NA est le nombre d'[http://fr.wikipedia.org/wiki/Nombre_d'Avogadro Avogadro] (6,022×10<sup>23</sup> mol<sup>-1</sup>) et kB est la constante de [http://fr.wikipedia.org/wiki/Constante_de_Stefan-Boltzmann Boltzmann] (1,38×10<sup>-23</sup> J/K) ; |
* T est la température absolue (en kelvin). | * T est la température absolue (en kelvin). | ||
| Ligne 66 : | Ligne 66 : | ||
[[Image:Gaz parfaits eq5.png]] | [[Image:Gaz parfaits eq5.png]] | ||
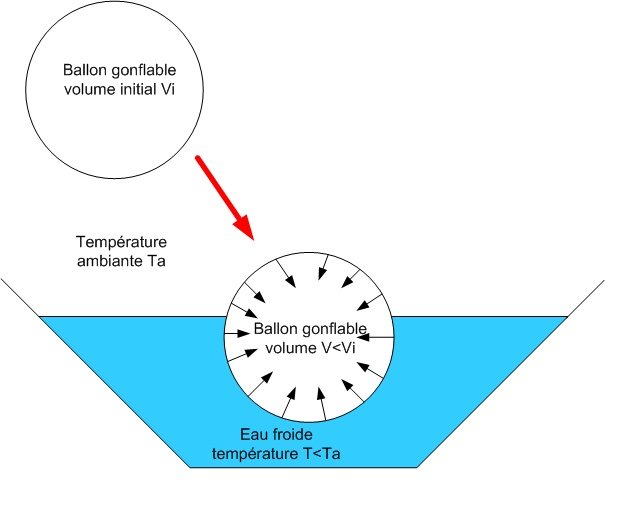
| - | A partir de cette formule, on peut voir directement que le produit pression volume est proportionnel à la température | + | A partir de cette formule, on peut voir directement que le produit pression volume est proportionnel à la température. De fait, si la température T diminue, le volume et la pression diminuent, le ballon se dégonfle. |
[[Image:Gaz parfaits froid.jpg]] | [[Image:Gaz parfaits froid.jpg]] | ||
Version du 9 novembre 2007 à 12:44
Sommaire |
Matériel
- Un ballon gonflable
- Un saladier
- Des glaçons
- De l’eau froide
- De l’eau chaude
- Du papier
- Un crayon
L'expérience
En vidéo
<googlevideo>-5797782857831411555</googlevideo>
La manipulation
- Gonfler un ballon un petit peu.
- Mettre le ballon dans un récipient rempli d’eau refroidie avec des glaçons.
- Observer la taille du ballon.
- Le mettre dans un récipient d’eau chaude.
- Observer de nouveau la taille du ballon.
Que voit-on ?
Lorsque le ballon est mis dans l’eau froide, il rétrécit, son volume diminue. Inversement, quand il est mis dans l’eau chaude, son volume augmente.
Explication
Lorsque le ballon est plongé dans de l’eau froide à une température inferieure à la température ambiante, son volume diminue. Au contraire, si le ballon est mis dans l’eau chaude, son volume augmente. Ces phénomènes physiques sont dus à la loi des gaz parfaits qui indique que le volume et la pression d’un gaz varient en fonction de la température de celui-ci :
- Si la température augmente , le volume et/ou la pression des gaz augmentent.
- Si la température diminue , le volume et/ou la pression des gaz diminuent.
Concepts scientifiques associés
L'état d'équilibre thermodynamique d'un gaz parfait est fixé ( n moles de molécules) par deux paramètres macroscopiques au choix. Les autres paramètres peuvent se calculer à partir des deux paramètres choisis par l'équation d'état. L'équation la plus couramment utilisée est l'équation des gaz parfaits, une équation thermo élastique.
Celle-ci peut s’écrire sous deux formes :
- Une vision macroscopique (le volume de gaz intervient) :
- Une vision microscopique (le nombre de molécules contenues dans une unité de volume intervient) :
où :
- p est la pression (en pascal)
- V est le volume occupé par le gaz (en mètre cube)
- n est la quantité de matière, en mole
- N est le nombre de particules
- R est la constante des gaz parfaits
R = 8,314 472 J/(K.mol) on a en fait R = NA•kB où NA est le nombre d'Avogadro (6,022×1023 mol-1) et kB est la constante de Boltzmann (1,38×10-23 J/K) ;
- T est la température absolue (en kelvin).
Une fois le ballon gonflé et fermé, la quantité de matière à l’intérieur de celui-ci est constante :
Et donc
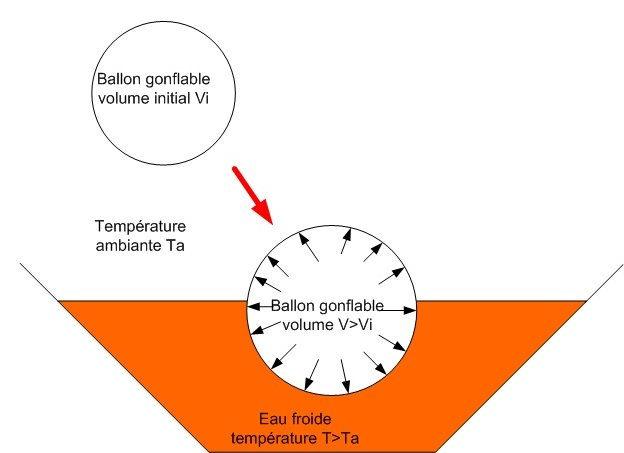
A partir de cette formule, on peut voir directement que le produit pression volume est proportionnel à la température. De fait, si la température T diminue, le volume et la pression diminuent, le ballon se dégonfle.
A l’inverse, si la température T augmente, le volume et la pression augmentent, se ballon se gonfle.