Ludion
De Wikidebrouillard.
| Ligne 14 : | Ligne 14 : | ||
<videoflash type="dailymotion">1KMFd01DydQJ6gU5H</videoflash> | <videoflash type="dailymotion">1KMFd01DydQJ6gU5H</videoflash> | ||
<videoflash type="dailymotion">x4tvzy&v3=1&related=1</videoflash> | <videoflash type="dailymotion">x4tvzy&v3=1&related=1</videoflash> | ||
| - | |||
== '''Explication''' == | == '''Explication''' == | ||
Version du 10 avril 2008 à 12:16
Sommaire |
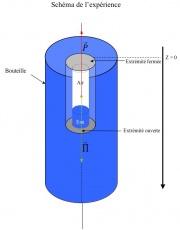
Matériel
-
 Une bouteille en plastique (soda, 1,5 litres)
Une bouteille en plastique (soda, 1,5 litres)
-
 De l'eau
De l'eau
- Un tube de stylo à bille (ou une paille
 )
)
-
 Un ou plusieurs trombones
Un ou plusieurs trombones
-
 Du scotche transparent
Du scotche transparent
-
 Des ciseaux
Des ciseaux
L'expérience
Explication
Nous cherchons à déterminer les conditions pour lesquelles le stylo coule ou flotte. Pour cela, la démonstration se décompose en deux étapes. Dans un premier temps nous allons déterminer les conditions de flottabilité du crayon. Puis nous nous intéresserons au déséquilibre provoqué par le manipulateur lorsqu'il presse la bouteille.
A l'extérieur du crayon
Bilan des forces qui s’appliquent sur le système crayon-trombone-air :
Il est soumis à deux forces :
• Son poids noté (dirigé vers le bas) : il a tendance à faire couler le système.
<math>\textstyle P=(m_{air}+m_{crayon}+m_{leste})g</math>
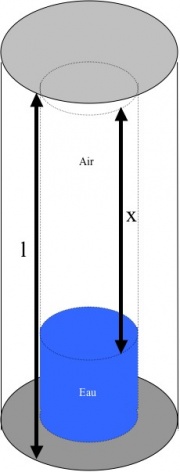
Avec : <math>\textstyle m_{air}=\rho_{air}.V_{air}=\rho_{air}.\pi r^{2}x</math>
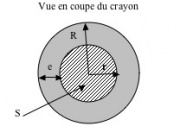
<math>\textstyle m_{crayon}=\rho_{crayon}.V_{crayon}=\rho_{crayon}.2\pi eRl</math>
Notations :
g = Accélération de la pesanteur <math>\rho</math> = Masse volumique V = Volume m = Masse
On obtient : <math>\textstyle P=(\rho_{air}.\pi r^{2}x+\rho_{crayon}.2\pi eRl+m_{leste})g</math>
• La poussée d’Archimède notée (dirigée vers le haut) : elle a tendance à faire flotter le système.
<math>\textstyle \Pi=-(V_{air}+V_{crayon})\rho_{eau}g</math>
On obtient :
<math>\textstyle \Pi=-(2\pi eRl+\pi r^{2}x)\rho_{eau}g</math>
Remarque : on néglige la poussée d’Archimède sur le leste étant donné le faible volume occupé par celui-ci.
Pour commencer, on considère le système à l’équilibre et on applique la première loi de Newton. Les forces sont toutes parallèles à l'axe z donc : <math>P-\Pi =0</math>
On obtient : <math>\textstyle P=(\rho_{air}.\pi r^{2}x+\rho_{crayon}.2\pi eRl+m_{leste})g-(2\pi eRl+\pi r^{2}x)\rho_{eau}g=0</math>
Soit : <math>x=\frac{2eRl}{r^{2}}\left(\frac{\rho_{eau}-\rho_{crayon}}{\rho_{air}-\rho_{eau}}\right)-\frac{m_{leste}}{\pi r^{2}(\rho_{air}-\rho_{eau})}</math> (1)
On pose : <math>x_{0}=\frac{2eRl}{r^{2}}\left(\frac{\rho_{eau}-\rho_{crayon}}{\rho_{air}-\rho_{eau}}\right)-\frac{m_{leste}}{\pi r^{2}(\rho_{air}-\rho_{eau})}</math>
A présent, on ce place dans le cas réel où le système ne se trouve pas forcément à l’équilibre Ces forces ce compensent alors plus ou moins. C’est ce qui provoque les mouvements du système dans la bouteille :
Le système monte lorsque : <math>\textstyle \Pi>P\Rightarrow x>x_{0}</math>
Le système descend lorsque : <math>\textstyle \Pi<P\Rightarrow x<x_{0}</math>
Le système est immobile lorsque : <math>\textstyle \Pi=P\Rightarrow x=x_{0}</math>
La constante <math>\textstyle x_{0}</math> représente donc la hauteur limite de la colonne d’air à l’intérieur du stylo en deçà de laquelle le système descend au fond de la bouteille. On peut donc prévoir, en observant le niveau d'eau dans le crayon et augmentant progressivement la pression de la main sur la bouteille, le moment où le "sous-marin va plonger".
On sait donc maintenant que c’est le volume d’air à l’intérieur du stylo qui conditionne le mouvement du système. Car seule la poussée d’Archimède, qui dépend de ce volume, peut contrer les effets de l’attraction gravitationnelle.
C’est bien le phénomène que l’on observe lors de l’expérience : lorsque l’on appuie sur les parois de la bouteille, l’eau monte à l’intérieur du crayon et le système descend.
Il se pose alors une nouvelle question : pourquoi le fait d’appuyer fait-il varier le niveau d’eau dans le crayon ?
A l'intérieur du crayon
Pour répondre à la question précédente, nous allons maintenant nous intéresser aux forces qui s’exercent sur la surface d’eau en contact avec l’air à l’intérieur du crayon. Ces forces résultent de la pression de l’air et de l’eau à cet endroit.
Pour simplifier le problème, nous considérons l’air comme un gaz parfait. Nous pouvons donc déterminer la pression <math>\textstyle P_{air}</math> à partir de la relation des gaz parfaits :
<math>\textstyle PV=nRT</math>
Où : P est la pression du gaz (Pa)
V est le volume occupé par le gaz (m3)
n est la quantité de gaz contenu dans ce volume (mole)
R est la constante des gaz parfaits : R = 8,314 Pa.m3.mole-1.K-1
T est la température du gaz (K)
Au départ, avant de plonger le stylo dans l’eau, le crayon contient moles de gaz à la pression atmosphérique <math>P_{atm}</math> , d’où :
<math>n_{air}=\frac{P_{atm}V}{RT}</math>
avec V : le volume intérieur (« vide ») du crayon
<math>n_{air}=\frac{P_{atm}.\pi r^{2}l}{RT}</math>
Et lorsque l’on plonge le stylo dans l’eau, la même quantité d’air est contenue à l’intérieur de celui-ci. En revanche, on remarque qu’à présent il y a un peu d’eau dans le crayon. Toujours d’après la loi des gaz parfaits, étant donné que seul le volume occupé par l’air a diminué c’est la pression qui a augmenté :
<math>P_{air}=\frac{n_{air}RT}{V_{air}}</math>
D’où : <math>P_{air}=P_{atm}\left(\frac{l}{x}\right)</math>
Intéressons nous maintenant à la pression exercée par la surface d’eau sur la surface d’air. Celle-ci se décompose en deux parties : la pression hydrostatique (celle subit par les plongeurs) et la pression exercée par le manipulateur.
Si on considère l’eau comme un fluide incompressible alors la totalité de la force exercée sur les parois de la bouteille est transmise sur la surface air-eau.
La pression hydrostatique est donnée par : <math>\textstyle P_{hydrostatique}=\rho_{eau}gz+P_{atm}</math>
La pression exercée par le manipulateur sur le fluide est donnée par : <math>P_{ext}=\frac{F_{ext}}{\pi r^{2}}</math>
D’où : <math>P_{eau}=\rho_{eau}gz+P_{atm}+\frac{F_{ext}}{\pi r^{2}}</math>
Prenons le système à l’équilibre : <math>\textstyle F_{air}=F_{eau}</math> C’est deux forces s’exercent sur une même surface. On en déduit que : <math>\textstyle P_{air}=P_{eau}</math>
D’où : <math>x=\frac{P_{atm}l}{\rho_{eau}gz+P_{atm}+P_{ext}}</math> (2)
On vient donc de relier la hauteur de la colonne d’air dans le stylo avec la pression exercée par le manipulateur sur la bouteille.
Conclusion
En combinant les équations (1) et (2), on peut alors définir la valeur minimum <math>\textstyle F_{0}</math> de <math>\textstyle F_{ext}</math> nécessaire pour faire couler le stylo :
Pour résumer :
Concepts scientifiques associés
ne pas hésiter à faire des liens avec l'encyclopédie :Wikipédia
Application : Lien avec le quotidien
Liens avec d'autres expériences
Comment l'animer ?
Liens avec des programmes d'animation
Comme par exemple "Debout les terriens", "foot'sciences", "6TdB", ...