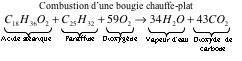Bougie dans le bocal
De Wikidebrouillard.
(→Liens avec d'autres expériences) |
|||
| (3 versions intermédiaires masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{avertissement}} | {{avertissement}} | ||
| - | {{vidéo|numérovidéo = <videoflash type=" | + | |
| - | + | {{vidéo|numérovidéo = <videoflash type="mediaspip" num="1">http://mediaspip.ptitdeb.infini.fr/IMG/flv/bougie_dans_le_bocal-encoded.flv|400|300</videoflash>}} | |
| - | + | ||
L'eau monte dans le bocal... oui mais pourquoi ? | L'eau monte dans le bocal... oui mais pourquoi ? | ||
| Ligne 9 : | Ligne 8 : | ||
* [[Image:Bougie.jpg|50px]] Des [[bougies]] | * [[Image:Bougie.jpg|50px]] Des [[bougies]] | ||
| - | * [[Image:Cartouche d'encre.jpg|50px]] Du colorant pour l'eau (cartouche [[encre]]) | + | * [[Image:Cartouche d'encre.jpg|50px]] Du colorant pour l'eau (cartouche d'[[encre]]) |
* [[Image:Allumettes.jpg|50px]] Des [[allumettes]] | * [[Image:Allumettes.jpg|50px]] Des [[allumettes]] | ||
* [[Image:Eau.jpg|50px]] De l'[[eau]] | * [[Image:Eau.jpg|50px]] De l'[[eau]] | ||
| Ligne 19 : | Ligne 18 : | ||
=== La manipulation === | === La manipulation === | ||
| - | + | * Mettre du colorant dans la soucoupe, ajouter de l'eau. | |
| - | + | ||
| - | + | ||
| - | + | * Placer la ou les bougies sur l'eau, les allumer. | |
| - | + | * Couvrir les bougies avec un bocal. | |
| - | + | ||
| - | + | ||
=== Que voit-on ? === | === Que voit-on ? === | ||
| - | |||
| - | + | Des bulles s’échappent par le bas du bocal. Il y a également de la buée sur les parois. Les bougies s’éteignent, et le niveau de l'eau monte. | |
| - | + | ||
| - | + | ||
| - | == ''' | + | == '''Explications''' == |
| - | === | + | === De manière simple === |
| - | Au premier abord, on pourrait penser que la flamme de la bougie consomme le dioxygène de l’air et donc réduit le volume d’air à l’intérieur du verre. Mais, c’est sans compter sur le fait que la réaction d’oxydation à l’origine de la flamme provoque également un dégagement de | + | Au premier abord, on pourrait penser que la flamme de la bougie consomme le dioxygène de l’air et donc réduit le volume d’air à l’intérieur du verre. Mais, c’est sans compter sur le fait que la réaction d’oxydation à l’origine de la flamme provoque également un dégagement de CO<sub>2</sub> et de la vapeur d’eau : |
[[Image:Bougiebocale_form1.jpg ]] | [[Image:Bougiebocale_form1.jpg ]] | ||
| Ligne 48 : | Ligne 40 : | ||
La vérité est ailleurs… | La vérité est ailleurs… | ||
| - | La bougie chauffe l’air contenu à l’intérieur du verre. Il se dilate et finit par s’échapper un peu du verre. Lorsque la bougie s’éteint, '''l’air se refroidit et se contracte en entraînant l’eau avec lui'''. C’est ainsi que le niveau | + | La bougie chauffe l’air contenu à l’intérieur du verre. Il se dilate et finit par s’échapper un peu du verre. Lorsque la bougie s’éteint, '''l’air se refroidit et se contracte en entraînant l’eau avec lui'''. C’est ainsi que le niveau du liquide monte. |
| + | |||
| + | === Allons plus loin dans l'explication === | ||
| - | |||
| - | ====Équilibre des pressions==== | + | ==== <font color="#158518">Équilibre des pressions</font> ==== |
Pour faciliter le raisonnement, nous allons considérer que l’air est un gaz parfait (ce qui loin d’être une aberration). Cela nous permet d’utiliser la loi des gaz parfaits : | Pour faciliter le raisonnement, nous allons considérer que l’air est un gaz parfait (ce qui loin d’être une aberration). Cela nous permet d’utiliser la loi des gaz parfaits : | ||
| Ligne 58 : | Ligne 51 : | ||
où : P est la pression du gaz (Pa) | où : P est la pression du gaz (Pa) | ||
| - | V est le volume occupé par le gaz ( | + | V est le volume occupé par le gaz (m<sup>3</sup>) |
| - | n est la quantité de gaz ( | + | n est la quantité de gaz (moles) |
| - | R est la constante des gaz parfaits (R=8,314 S.I.) | + | R est la constante des gaz parfaits (R = 8,314 S.I.) |
T est la température du gaz (K) | T est la température du gaz (K) | ||
| Ligne 68 : | Ligne 61 : | ||
Cette relation nous permet de relier la température au volume occupé par le gaz. On remarque que, pour une quantité de gaz donnée à pression constante, lorsque que la température T augmente, alors automatiquement V augmente : il prend plus de place (dilatation). | Cette relation nous permet de relier la température au volume occupé par le gaz. On remarque que, pour une quantité de gaz donnée à pression constante, lorsque que la température T augmente, alors automatiquement V augmente : il prend plus de place (dilatation). | ||
| - | Dans notre cas, on emprisonne une certaine quantité d’air à l’intérieur du verre. En temps normal, cet air ne peut pas s’échapper du | + | Dans notre cas, on emprisonne une certaine quantité d’air à l’intérieur du verre. En temps normal, cet air ne peut pas s’échapper du bocal à moins qu'on ne sorte celui-ci de l’eau. La flamme de la bougie placée à l’intérieur dégage de la chaleur. Cette chaleur est transmise à l’air principalement par rayonnement, c’est-à-dire par « frottement » de l’air sur la flamme. L’air s’échauffe et prend donc plus de place selon la loi des gaz parfaits. Il se dilate tellement que le volume du verre ne suffit plus à le contenir entièrement et il s’échappe par le bas du bocal. |
| - | Une question se pose alors : pourquoi l’air à l’intérieur du | + | Une question se pose alors : pourquoi l’air à l’intérieur du bocal ne se comprime-t-il pas ? |
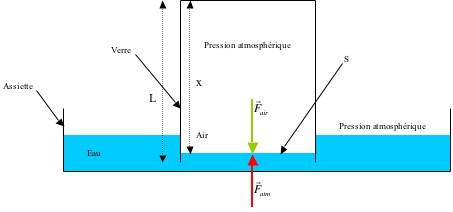
| - | Pour répondre à cette question faisons le bilan des forces qui s’exercent sur le système. Pour cela, on considère l’ensemble du dispositif sans la bougie qui n’intervient pas dans le bilan des forces de pression. | + | Pour répondre à cette question, faisons le bilan des forces qui s’exercent sur le système. Pour cela, on considère l’ensemble du dispositif sans la bougie qui n’intervient pas dans le bilan des forces de pression. |
[[Image:Bougiebocal_pct1.jpg ]] | [[Image:Bougiebocal_pct1.jpg ]] | ||
| - | + | À tout instant, il y a équilibre entre les forces exercées par l’air à l’extérieur et à l’intérieur du verre étant donné que la pression est la même. Donc : | |
Initialement (à t=0): | Initialement (à t=0): | ||
| Ligne 88 : | Ligne 81 : | ||
[[Image:Bougiebocal_pct2.jpg ]] | [[Image:Bougiebocal_pct2.jpg ]] | ||
| - | La flamme réchauffe l’air à l’intérieur du verre. Cet air se dilate et se met, par manque de place, à déborder du verre. Le gaz qui s’échappe alors ne peut plus être récupéré car la couche d’eau l’empêche de rentrer à nouveau. On | + | La flamme réchauffe l’air à l’intérieur du verre. Cet air se dilate et se met, par manque de place, à déborder du verre. Le gaz qui s’échappe alors ne peut plus être récupéré car la couche d’eau l’empêche de rentrer à nouveau. On appelle n la quantité de gaz qui s’échappe du verre. On peut donc écrire : |
Avec : | Avec : | ||
| - | + | À t= t1 : | |
[[Image:Bougiebocal_pct3.jpg ]] | [[Image:Bougiebocal_pct3.jpg ]] | ||
| Ligne 102 : | Ligne 95 : | ||
La température de l’air diminue et tend vers celle de la pièce (ici 20°C). Donc toujours d’après la même loi, cela entraîne une diminution du volume occupé par le gaz. | La température de l’air diminue et tend vers celle de la pièce (ici 20°C). Donc toujours d’après la même loi, cela entraîne une diminution du volume occupé par le gaz. | ||
| - | Étant donné que la quantité de gaz a diminué durant la phase précédente, le volume va être inférieur au volume initial à la fin du refroidissement. C’est la pression atmosphérique qui « appuie » sur l’eau à l’extérieur du verre pour permettre l’égalité : | + | Étant donné que la quantité de gaz a diminué durant la phase précédente, le volume va être inférieur au volume initial à la fin du refroidissement. C’est la pression atmosphérique qui « appuie » sur l’eau à l’extérieur du verre pour permettre l’égalité : ....... |
| - | Lorsque | + | Lorsque ......, on peut écrire : |
[[Image:Bougiebocal_pct4.jpg]] | [[Image:Bougiebocal_pct4.jpg]] | ||
| - | La différence de hauteur de la colonne d’eau s’écrit donc : | + | La différence de hauteur de la colonne d’eau s’écrit donc : ...... |
| - | Remarque : la condensation sur les parois du verre indique la présence de vapeur d’eau. Cette vapeur en se condensant va absorber une partie de l’énergie thermique du système. On peut définir la chaleur absorbée par ce changement d’état telle que : | + | Remarque : la condensation sur les parois du verre indique la présence de vapeur d’eau. Cette vapeur en se condensant va absorber une partie de l’énergie thermique du système. On peut définir la chaleur absorbée par ce changement d’état telle que : ..... |
| - | Soit une variation de température de : | + | Soit une variation de température de : ..... |
| - | Dans notre cas, on trouve que la condensation de l’eau participe au refroidissement du système à hauteur de 0,17°C | + | Dans notre cas, on trouve que la condensation de l’eau participe au refroidissement du système à hauteur de 0,17°C (.....) |
Voilà donc pour l’interprétation théorique de ce phénomène. À présent il serait utile de pouvoir le quantifier. Pour cela, on utilise un montage différent. En effet, le seul paramètre « non observable à l’œil nu » reste la température à l’intérieur du verre. Pour la mesurer, on utilisera un montage différent qui permet de faire varier la température de l’air contenu à l’intérieur d’un Erlenmeyer beaucoup plus lentement qu’avec une bougie. Ce montage est présenté ci-dessous. | Voilà donc pour l’interprétation théorique de ce phénomène. À présent il serait utile de pouvoir le quantifier. Pour cela, on utilise un montage différent. En effet, le seul paramètre « non observable à l’œil nu » reste la température à l’intérieur du verre. Pour la mesurer, on utilisera un montage différent qui permet de faire varier la température de l’air contenu à l’intérieur d’un Erlenmeyer beaucoup plus lentement qu’avec une bougie. Ce montage est présenté ci-dessous. | ||
| Ligne 138 : | Ligne 131 : | ||
Pour le matériel et les conditions suivantes : | Pour le matériel et les conditions suivantes : | ||
| - | *Erlenmeyer de 150 mL | + | * Erlenmeyer de 150 mL |
| - | *Bougie d’anniversaire | + | * Bougie d’anniversaire |
| - | *Pression atmosphérique : 1013 hPa | + | * Pression atmosphérique : 1013 hPa |
| - | Les résultats indiquent que l’air doit être porté à environ 80°C à l’intérieur du verre pour obtenir le même résultat qu’avec une bougie. Ces conditions correspondent à peu près à | + | Les résultats indiquent que l’air doit être porté à environ 80°C à l’intérieur du verre pour obtenir le même résultat qu’avec une bougie. Ces conditions correspondent à peu près à celles de l’expérience habituelle (avec un verre d’eau). |
Mais attention, les phénomènes thermodynamiques décrits ci-dessus ne sont pas les seuls à intervenir. Certes d’après l’expérience précédente, on peut considérer qu’ils sont principalement à l’origine de la montée de l’eau dans le verre. Mais il est quand même intéressant d’évoquer d’autres phénomènes qui se produisent en même temps. | Mais attention, les phénomènes thermodynamiques décrits ci-dessus ne sont pas les seuls à intervenir. Certes d’après l’expérience précédente, on peut considérer qu’ils sont principalement à l’origine de la montée de l’eau dans le verre. Mais il est quand même intéressant d’évoquer d’autres phénomènes qui se produisent en même temps. | ||
| - | ==== | + | ==== <font color="#158518">O<sub>2</sub> vs CO<sub>2</sub></font> ==== |
| - | La combustion de la bougie | + | La combustion de la bougie consomme du dioxygène pour rejeter du CO<sub>2</sub> mais pas dans les mêmes proportions. D’après l’équation de la réaction, pour 59 molécules de O<sub>2</sub> consommées, il y a formation de 43 molécules de CO<sub>2</sub>. Or on peut raisonnablement considérer que ces deux gaz occupent la même « place », autrement dit que leur volume molaire est identique (on fait généralement cette considération pour tous les gaz). Le volume de gaz à l’intérieur du verre va donc varier également pour ces raisons. |
| Ligne 154 : | Ligne 147 : | ||
Pour cela nous allons utiliser l’équation de combustion de la bougie et introduire un certain nombre de notations pour différentes grandeurs. | Pour cela nous allons utiliser l’équation de combustion de la bougie et introduire un certain nombre de notations pour différentes grandeurs. | ||
| - | État initial : | + | État initial : ..... |
| - | État final : | + | État final : ..... |
n désigne la quantité de matière en moles de la molécule correspondante | n désigne la quantité de matière en moles de la molécule correspondante | ||
| - | désigne la quantité de matière qui a été transférée au cours de la réaction (car : « Rien ne se perd, tout se transforme » !) | + | .....désigne la quantité de matière qui a été transférée au cours de la réaction (car : « Rien ne se perd, tout se transforme » !) |
| - | Cette dernière grandeur ne peut être calculée qu’en connaissant l’état final de la réaction. Ici, la réaction s’arrête lorsque l’ensemble du dioxygène | + | Cette dernière grandeur ne peut être calculée qu’en connaissant l’état final de la réaction. Ici, la réaction s’arrête lorsque l’ensemble du dioxygène a été consommé. Il nous suffit donc de calculer la quantité de O<sub>2</sub> présente, avant le début de la réaction, dans le verre. On peut alors avoir accès à ..... . |
On fera désormais l’approximation suivante pour simplifier les calculs : l’air est sec (humidité relative de 0 %). | On fera désormais l’approximation suivante pour simplifier les calculs : l’air est sec (humidité relative de 0 %). | ||
| - | Dans l’air sec, il y a environ 20,95% de | + | Dans l’air sec, il y a environ 20,95% de O<sub>2</sub> et 0,0382% de CO<sub>2</sub>. |
Nous connaissons le volume intérieur de notre verre : | Nous connaissons le volume intérieur de notre verre : | ||
| Ligne 171 : | Ligne 164 : | ||
r = rayon du verre (même remarque) | r = rayon du verre (même remarque) | ||
| - | Les quantités de | + | Les quantités de O<sub>2</sub> et de CO<sub>2</sub> peuvent être calculées : ....... |
| - | Nous venons donc de déterminer les conditions initiales de ce problème. Intéressons-nous à présent au remplacement du | + | Nous venons donc de déterminer les conditions initiales de ce problème. Intéressons-nous à présent au remplacement du O<sub>2</sub> par le CO<sub>2</sub>. |
| - | Pour déterminer la quantité de | + | Pour déterminer la quantité de CO<sub>2</sub> que produit la combustion, nous pouvons calculer le nombre de fois que va se produire la réaction telle qu’elle est décrite un peu plus haut. |
| - | Initialement, le nombre de molécules de | + | Initialement, le nombre de molécules de O<sub>2</sub> et de CO<sub>2</sub> présentes dans le verre est respectivement de : ...... |
| - | et | + | et ....... |
| - | Selon l’équation de réaction, celle-ci va pouvoir se produire y fois : | + | Selon l’équation de réaction, celle-ci va pouvoir se produire y fois : ....... |
| - | Toujours selon cette même équation, le volume de | + | Toujours selon cette même équation, le volume de C0<sub>2</sub> produit au cours de la réaction est de : ....... |
| - | D’où la variation de volume due au remplacement du | + | D’où la variation de volume due au remplacement du 0<sub>2</sub> par le C0<sub>2</sub> : ....... |
| - | Étant donné que : | + | Étant donné que ...... : alors on peut affirmer que le remplacement du 0<sub>2</sub> par le C0<sub>2</sub> implique forcément une diminution du volume et donc une augmentation de la quantité d’eau à l’intérieur du verre (pour respecter l’équilibre thermodynamique). |
Pour un « verre à moutarde », le calcul donne une élévation due à ce phénomène d’environ 4 mm du niveau d’eau dans le verre. Il n’est donc pas négligeable. | Pour un « verre à moutarde », le calcul donne une élévation due à ce phénomène d’environ 4 mm du niveau d’eau dans le verre. Il n’est donc pas négligeable. | ||
| - | ====Vaporisation de l’eau==== | + | ==== <font color="#158518">Vaporisation de l’eau</font> ==== |
À présent, on peut légitimement se poser la question de la place qu’occupe dans le verre la vapeur d’eau créée au cours de la combustion. | À présent, on peut légitimement se poser la question de la place qu’occupe dans le verre la vapeur d’eau créée au cours de la combustion. | ||
| - | De la même manière que précédemment, on peut déterminer la quantité de vapeur d’eau créée : | + | De la même manière que précédemment, on peut déterminer la quantité de vapeur d’eau créée : ...... |
| + | |||
| + | Selon l’équation de réaction : ...... | ||
| - | |||
On considère pour simplifier que l’ensemble des molécules d’eau retourne à l’état liquide. Cette supposition n’est pas absurde étant donné que la température est inférieure à 100°C (température de vaporisation à la pression atmosphérique) dans tout le verre excepté dans une petite région au-dessus de la flamme. | On considère pour simplifier que l’ensemble des molécules d’eau retourne à l’état liquide. Cette supposition n’est pas absurde étant donné que la température est inférieure à 100°C (température de vaporisation à la pression atmosphérique) dans tout le verre excepté dans une petite région au-dessus de la flamme. | ||
| - | Le volume d’eau liquide correspondant est : | + | Le volume d’eau liquide correspondant est : ...... |
Toujours dans notre exemple, on a calculé un apport de 23μL en eau. Cette quantité est très petite par rapport à la quantité d’eau déjà présente. Ce phénomène est donc négligeable. | Toujours dans notre exemple, on a calculé un apport de 23μL en eau. Cette quantité est très petite par rapport à la quantité d’eau déjà présente. Ce phénomène est donc négligeable. | ||
| - | ====Dissolution du | + | ==== <font color="#158518">Dissolution du C0<sub>2</sub></font> ==== |
| - | On peut également supposer qu’une partie du | + | On peut également supposer qu’une partie du C0<sub>2</sub> s’est dissout dans l’eau et donc que le volume occupé par le gaz diminue. En effet, certains gaz se dissolvent très bien dans l’eau (exemple : l’oxygène pour les poissons). C’est le cas du dioxyde de carbone. Pour déterminer les quantités mises en jeu, on utilise la loi de Henry. Mais cette loi ne peut s’appliquer que si le gaz est en contact prolongé avec le solvant. Ici la réaction étant très brève, le C0<sub>2</sub> n’a pas vraiment le temps de se dissoudre de manière significative dans l’eau. On négligera là encore ce phénomène. |
Tableau récapitulatif : | Tableau récapitulatif : | ||
| - | Phénomène Équilibre des pressions Condensation de l’eau Combustion de la bougie Vaporisation de l’eau Dissolution du | + | Phénomène Équilibre des pressions Condensation de l’eau Combustion de la bougie Vaporisation de l’eau Dissolution du C0<sub>2</sub> |
| - | Effet sur le système Une partie de l’air est chassée du verre lorsque l’on chauffe l’air. Le retour aux conditions initiales implique une diminution du volume. L’eau en se condensant participe au refroidissement du système. La combustion consomme de l’oxygène et rejette du CO2. Le remplacement d’un gaz par l’autre implique une diminution du volume occupé. La combustion de la bougie dégage de la vapeur d’eau qui occupe un certain volume dans le verre. Le | + | Effet sur le système Une partie de l’air est chassée du verre lorsque l’on chauffe l’air. Le retour aux conditions initiales implique une diminution du volume. L’eau en se condensant participe au refroidissement du système. La combustion consomme de l’oxygène et rejette du CO2. Le remplacement d’un gaz par l’autre implique une diminution du volume occupé. La combustion de la bougie dégage de la vapeur d’eau qui occupe un certain volume dans le verre. Le C0<sub>2</sub> en présence d’eau peut se dissoudre dans celle-ci et faire diminuer le volume de gaz présent dans le verre. |
Négligeable ? C’est le phénomène le plus important. Il fait monter le niveau de l’eau de quelques centimètres. Ces effets ne sont pas importants et ne modifient en rien le résultat final. Il permet de faire monter le niveau d’eau de quelques millimètres. Ce phénomène est négligeable car il est compensé par la condensation. Le gaz ne reste pas suffisamment longtemps en contact avec le gaz pour avoir une influence. | Négligeable ? C’est le phénomène le plus important. Il fait monter le niveau de l’eau de quelques centimètres. Ces effets ne sont pas importants et ne modifient en rien le résultat final. Il permet de faire monter le niveau d’eau de quelques millimètres. Ce phénomène est négligeable car il est compensé par la condensation. Le gaz ne reste pas suffisamment longtemps en contact avec le gaz pour avoir une influence. | ||
| Ligne 220 : | Ligne 214 : | ||
== '''Liens avec d'autres expériences''' == | == '''Liens avec d'autres expériences''' == | ||
| - | *[[Air]] : plusieurs expériences liées à l'air dans cette balade thématique. | + | * [[Air]] : plusieurs expériences liées à l'air dans cette balade thématique. |
* [[Bouchon qui se soulève]] | * [[Bouchon qui se soulève]] | ||
* [[Comment faire entrer un oeuf dans un bocal ?]] | * [[Comment faire entrer un oeuf dans un bocal ?]] | ||
* [[Hémisphères de Magdebourg]] | * [[Hémisphères de Magdebourg]] | ||
| + | * [[Le bocal sans la bougie]] | ||
== '''Applications : Liens avec le quotidien''' == | == '''Applications : Liens avec le quotidien''' == | ||
| Ligne 229 : | Ligne 224 : | ||
[[Catégorie:Physique]] | [[Catégorie:Physique]] | ||
| + | [[Catégorie:thermodynamique]] | ||
[[Catégorie:Chimie]] | [[Catégorie:Chimie]] | ||
| - | [[Catégorie: | + | [[Catégorie:chimie réactionnelle]] |
| + | [[Catégorie:oxydo-réduction]] | ||
| + | [[Catégorie:combustion]] | ||
[[Catégorie:Contenus à développer]] | [[Catégorie:Contenus à développer]] | ||
[[Catégorie:Fiche à Valider]] | [[Catégorie:Fiche à Valider]] | ||
[[Catégorie:expérience]] | [[Catégorie:expérience]] | ||
| + | [[Catégorie:mediaspip]] | ||
Version actuelle en date du 4 avril 2013 à 09:28
L'eau monte dans le bocal... oui mais pourquoi ?
Sommaire |
Matériel
-
 Des bougies
Des bougies
-
 Du colorant pour l'eau (cartouche d'encre)
Du colorant pour l'eau (cartouche d'encre)
-
 Des allumettes
Des allumettes
-
 De l'eau
De l'eau
-
 Un bocal assez grand ou
Un bocal assez grand ou un verre
-
 Une soucoupe ou une assiette
Une soucoupe ou une assiette
L'expérience
La manipulation
- Mettre du colorant dans la soucoupe, ajouter de l'eau.
- Placer la ou les bougies sur l'eau, les allumer.
- Couvrir les bougies avec un bocal.
Que voit-on ?
Des bulles s’échappent par le bas du bocal. Il y a également de la buée sur les parois. Les bougies s’éteignent, et le niveau de l'eau monte.
Explications
De manière simple
Au premier abord, on pourrait penser que la flamme de la bougie consomme le dioxygène de l’air et donc réduit le volume d’air à l’intérieur du verre. Mais, c’est sans compter sur le fait que la réaction d’oxydation à l’origine de la flamme provoque également un dégagement de CO2 et de la vapeur d’eau :
Il n’est donc pas question ici d’une diminution du volume d’air due à cette réaction chimique.
La vérité est ailleurs…
La bougie chauffe l’air contenu à l’intérieur du verre. Il se dilate et finit par s’échapper un peu du verre. Lorsque la bougie s’éteint, l’air se refroidit et se contracte en entraînant l’eau avec lui. C’est ainsi que le niveau du liquide monte.
Allons plus loin dans l'explication
Équilibre des pressions
Pour faciliter le raisonnement, nous allons considérer que l’air est un gaz parfait (ce qui loin d’être une aberration). Cela nous permet d’utiliser la loi des gaz parfaits :
où : P est la pression du gaz (Pa)
V est le volume occupé par le gaz (m3)
n est la quantité de gaz (moles)
R est la constante des gaz parfaits (R = 8,314 S.I.)
T est la température du gaz (K)
Cette relation nous permet de relier la température au volume occupé par le gaz. On remarque que, pour une quantité de gaz donnée à pression constante, lorsque que la température T augmente, alors automatiquement V augmente : il prend plus de place (dilatation).
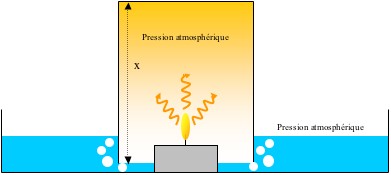
Dans notre cas, on emprisonne une certaine quantité d’air à l’intérieur du verre. En temps normal, cet air ne peut pas s’échapper du bocal à moins qu'on ne sorte celui-ci de l’eau. La flamme de la bougie placée à l’intérieur dégage de la chaleur. Cette chaleur est transmise à l’air principalement par rayonnement, c’est-à-dire par « frottement » de l’air sur la flamme. L’air s’échauffe et prend donc plus de place selon la loi des gaz parfaits. Il se dilate tellement que le volume du verre ne suffit plus à le contenir entièrement et il s’échappe par le bas du bocal.
Une question se pose alors : pourquoi l’air à l’intérieur du bocal ne se comprime-t-il pas ?
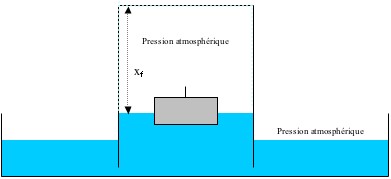
Pour répondre à cette question, faisons le bilan des forces qui s’exercent sur le système. Pour cela, on considère l’ensemble du dispositif sans la bougie qui n’intervient pas dans le bilan des forces de pression.
À tout instant, il y a équilibre entre les forces exercées par l’air à l’extérieur et à l’intérieur du verre étant donné que la pression est la même. Donc :
Initialement (à t=0):
La température de l’air à l’intérieur du verre est la même que celle de l’air ambiant :
Donc d’après la loi des gaz parfaits :
Pour 0 < t < t1 :
La flamme réchauffe l’air à l’intérieur du verre. Cet air se dilate et se met, par manque de place, à déborder du verre. Le gaz qui s’échappe alors ne peut plus être récupéré car la couche d’eau l’empêche de rentrer à nouveau. On appelle n la quantité de gaz qui s’échappe du verre. On peut donc écrire :
Avec :
À t= t1 :
L’ensemble de l’oxygène présent dans l’air emprisonné dans le verre a été consommé et la flamme s’éteint. On a alors :
Pour t > t1 :
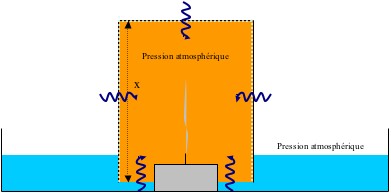
La température de l’air diminue et tend vers celle de la pièce (ici 20°C). Donc toujours d’après la même loi, cela entraîne une diminution du volume occupé par le gaz.
Étant donné que la quantité de gaz a diminué durant la phase précédente, le volume va être inférieur au volume initial à la fin du refroidissement. C’est la pression atmosphérique qui « appuie » sur l’eau à l’extérieur du verre pour permettre l’égalité : .......
Lorsque ......, on peut écrire :
La différence de hauteur de la colonne d’eau s’écrit donc : ......
Remarque : la condensation sur les parois du verre indique la présence de vapeur d’eau. Cette vapeur en se condensant va absorber une partie de l’énergie thermique du système. On peut définir la chaleur absorbée par ce changement d’état telle que : .....
Soit une variation de température de : .....
Dans notre cas, on trouve que la condensation de l’eau participe au refroidissement du système à hauteur de 0,17°C (.....)
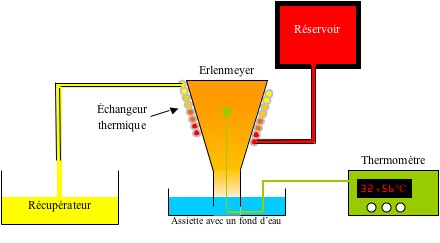
Voilà donc pour l’interprétation théorique de ce phénomène. À présent il serait utile de pouvoir le quantifier. Pour cela, on utilise un montage différent. En effet, le seul paramètre « non observable à l’œil nu » reste la température à l’intérieur du verre. Pour la mesurer, on utilisera un montage différent qui permet de faire varier la température de l’air contenu à l’intérieur d’un Erlenmeyer beaucoup plus lentement qu’avec une bougie. Ce montage est présenté ci-dessous.
Pourquoi ne pas utiliser le thermomètre avec la bougie ?
Lorsque la bougie chauffe l’air, elle ne le fait pas de manière homogène. La température est beaucoup plus importante juste au-dessus de la flamme. Pour s’en convaincre, il suffit de placer une brindille à 1 cm du sommet de la flamme. Sur le côté, elle ne brûle pas mais au-dessus oui. Or ce qui nous intéresse c’est la température de l’air à l’intérieur du récipient. Nous pourrons donc ne donner qu’un ordre d’idée de la température de l’air qui provoquerait un phénomène identique, si elle était homogène.
Protocole :
On effectue d’abord l’expérience habituelle avec une bougie d’anniversaire et l’Erlenmeyer à la place du verre. On note le niveau atteint par l’eau après le retour à température ambiante.
Puis on installe l’échangeur thermique (comme sur le schéma) au niveau du récipient. On place le thermocouple accroché à la bougie au milieu du récipient. On le branche à un multimètre.
On fait couler de l’eau à la température voulue à l’intérieur de l’échangeur. On attend que la température se stabilise et on la note.
On fait alors couler de l’eau à température ambiante dans l’échangeur pour accélérer le refroidissement. On attend que la température se stabilise et l’on note le niveau atteint par l’eau dans le récipient.
La température désirée est obtenue lorsque les niveaux sont identiques pour les deux expériences.
Pour le matériel et les conditions suivantes :
- Erlenmeyer de 150 mL
- Bougie d’anniversaire
- Pression atmosphérique : 1013 hPa
Les résultats indiquent que l’air doit être porté à environ 80°C à l’intérieur du verre pour obtenir le même résultat qu’avec une bougie. Ces conditions correspondent à peu près à celles de l’expérience habituelle (avec un verre d’eau).
Mais attention, les phénomènes thermodynamiques décrits ci-dessus ne sont pas les seuls à intervenir. Certes d’après l’expérience précédente, on peut considérer qu’ils sont principalement à l’origine de la montée de l’eau dans le verre. Mais il est quand même intéressant d’évoquer d’autres phénomènes qui se produisent en même temps.
O2 vs CO2
La combustion de la bougie consomme du dioxygène pour rejeter du CO2 mais pas dans les mêmes proportions. D’après l’équation de la réaction, pour 59 molécules de O2 consommées, il y a formation de 43 molécules de CO2. Or on peut raisonnablement considérer que ces deux gaz occupent la même « place », autrement dit que leur volume molaire est identique (on fait généralement cette considération pour tous les gaz). Le volume de gaz à l’intérieur du verre va donc varier également pour ces raisons.
Nous allons tenter de quantifier ce phénomène.
Pour cela nous allons utiliser l’équation de combustion de la bougie et introduire un certain nombre de notations pour différentes grandeurs.
État initial : .....
État final : .....
n désigne la quantité de matière en moles de la molécule correspondante .....désigne la quantité de matière qui a été transférée au cours de la réaction (car : « Rien ne se perd, tout se transforme » !)
Cette dernière grandeur ne peut être calculée qu’en connaissant l’état final de la réaction. Ici, la réaction s’arrête lorsque l’ensemble du dioxygène a été consommé. Il nous suffit donc de calculer la quantité de O2 présente, avant le début de la réaction, dans le verre. On peut alors avoir accès à ..... .
On fera désormais l’approximation suivante pour simplifier les calculs : l’air est sec (humidité relative de 0 %).
Dans l’air sec, il y a environ 20,95% de O2 et 0,0382% de CO2.
Nous connaissons le volume intérieur de notre verre : Où : h = hauteur du verre (seulement de sa partie intérieure) r = rayon du verre (même remarque)
Les quantités de O2 et de CO2 peuvent être calculées : .......
Nous venons donc de déterminer les conditions initiales de ce problème. Intéressons-nous à présent au remplacement du O2 par le CO2.
Pour déterminer la quantité de CO2 que produit la combustion, nous pouvons calculer le nombre de fois que va se produire la réaction telle qu’elle est décrite un peu plus haut.
Initialement, le nombre de molécules de O2 et de CO2 présentes dans le verre est respectivement de : ......
et .......
Selon l’équation de réaction, celle-ci va pouvoir se produire y fois : .......
Toujours selon cette même équation, le volume de C02 produit au cours de la réaction est de : .......
D’où la variation de volume due au remplacement du 02 par le C02 : .......
Étant donné que ...... : alors on peut affirmer que le remplacement du 02 par le C02 implique forcément une diminution du volume et donc une augmentation de la quantité d’eau à l’intérieur du verre (pour respecter l’équilibre thermodynamique).
Pour un « verre à moutarde », le calcul donne une élévation due à ce phénomène d’environ 4 mm du niveau d’eau dans le verre. Il n’est donc pas négligeable.
Vaporisation de l’eau
À présent, on peut légitimement se poser la question de la place qu’occupe dans le verre la vapeur d’eau créée au cours de la combustion.
De la même manière que précédemment, on peut déterminer la quantité de vapeur d’eau créée : ......
Selon l’équation de réaction : ......
On considère pour simplifier que l’ensemble des molécules d’eau retourne à l’état liquide. Cette supposition n’est pas absurde étant donné que la température est inférieure à 100°C (température de vaporisation à la pression atmosphérique) dans tout le verre excepté dans une petite région au-dessus de la flamme.
Le volume d’eau liquide correspondant est : ......
Toujours dans notre exemple, on a calculé un apport de 23μL en eau. Cette quantité est très petite par rapport à la quantité d’eau déjà présente. Ce phénomène est donc négligeable.
Dissolution du C02
On peut également supposer qu’une partie du C02 s’est dissout dans l’eau et donc que le volume occupé par le gaz diminue. En effet, certains gaz se dissolvent très bien dans l’eau (exemple : l’oxygène pour les poissons). C’est le cas du dioxyde de carbone. Pour déterminer les quantités mises en jeu, on utilise la loi de Henry. Mais cette loi ne peut s’appliquer que si le gaz est en contact prolongé avec le solvant. Ici la réaction étant très brève, le C02 n’a pas vraiment le temps de se dissoudre de manière significative dans l’eau. On négligera là encore ce phénomène.
Tableau récapitulatif :
Phénomène Équilibre des pressions Condensation de l’eau Combustion de la bougie Vaporisation de l’eau Dissolution du C02 Effet sur le système Une partie de l’air est chassée du verre lorsque l’on chauffe l’air. Le retour aux conditions initiales implique une diminution du volume. L’eau en se condensant participe au refroidissement du système. La combustion consomme de l’oxygène et rejette du CO2. Le remplacement d’un gaz par l’autre implique une diminution du volume occupé. La combustion de la bougie dégage de la vapeur d’eau qui occupe un certain volume dans le verre. Le C02 en présence d’eau peut se dissoudre dans celle-ci et faire diminuer le volume de gaz présent dans le verre. Négligeable ? C’est le phénomène le plus important. Il fait monter le niveau de l’eau de quelques centimètres. Ces effets ne sont pas importants et ne modifient en rien le résultat final. Il permet de faire monter le niveau d’eau de quelques millimètres. Ce phénomène est négligeable car il est compensé par la condensation. Le gaz ne reste pas suffisamment longtemps en contact avec le gaz pour avoir une influence.
Concepts scientifiques associés
Pourquoi l'eau monte dans "la bougie dans le bocal"? : émission d'hypothèses
Liens avec d'autres expériences
- Air : plusieurs expériences liées à l'air dans cette balade thématique.
- Bouchon qui se soulève
- Comment faire entrer un oeuf dans un bocal ?
- Hémisphères de Magdebourg
- Le bocal sans la bougie
Applications : Liens avec le quotidien
- Dernière modification de cette page le 4 avril 2013 à 09:28.
- Cette page a été consultée 134 721 fois.
- Contenu disponible sous Creative Commons - Paternite Partage a l'identique (CC-BY-SA).
- Politique de confidentialité
- À propos de Wikidebrouillard
- Avertissements